A radio receiver receives radio telegraphic signals in Morse code in the form of sinusoidal wave packets (Fig.36.4). The inductance of the circuit is 100 μ II, the capacitance is 250 μμ F and the resistanc is 0.2 ohm. Find the interval betweent the impluse πsp needed to prevent two adjacent signals from merging.
Assuming the duration of the "dot" signal to be π.=1.5πsp and that of the "dash" πdash=4.5sp find the maximum amount of information that can be transmitted per unit time.
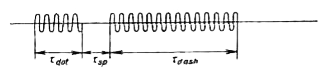
A radio receiver receives radio telegraphic signals in Morse code in the form of sinusoidal wave packets (Fig.36.4). The inductance of the circuit is 100 mu II, the capacitance is 250 mu mu F and the resistanc is 0.2 ohm. Find the interval betweent the impluse pi(sp) needed to prevent two adjacent signals from merging. Assuming the duration of the

Text Solution
Verified by Experts

The correct Answer is:πap=2QTθπ=2×106(3)T0=2 ms; not greater than N = ω−(0)16Q=125 pulses/s.

To prevent the merging of two successive impulses the interval between them should be appreciably longer than the time of damping of the first impulse and the build - up time of the second. i.e.
πsp>2π≈4Q/ω0
To find the maximum volume of information transmitted per second, one should take into account that such information should be made up of N1 dots and N2 dashes, N1+N2, where N is the amount of information . But usually on the average N1≈N2≈N/2.
1s=N(1)τ1+N2τ2+Nτsp(1.52+4.52+1)=4Nτsp≈16NQω0
Hence we find the amount of information, N<R/16L.

Updated on:21/07/2023
Doubtnut Promotions Banner
|