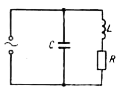
Plot the vector diagram for currents in the circuit shown in Fig. 36.11 a and find the current in the unbranched section of the circuit. What is the condition for the current in the unbranched section of be a minimum? What is the phase shift between the voltage and the current in general, and at resonance?
Text Solution
The correct Answer is:The current in the unbranched section of the circuit is
I=U√R2C2ω2+(LCω2−1)2=UR
⎷γ2/Q2+(γ2−1)21+Q2γ2
It is minimum at resonance (γ=ωωe=1
The vector diagram is shown in Fig.36.11 b (see problem 36.9) where
Z0=√R2+L2ω2,cosφ0=R/Z0.sinφ0=Lω/Z0

It is clear from the diagram that
I2=I20+I2C−2I0Icosα
but since α−(π/2)−φ0, it follows that
I2=I20+I2C−2I0ICsinφ0
Substituting the values of the currents and sinφ0, we obtain after some simple transformations the required effective value of the current in the unbranched section of the circuit.
From the vector diagram cosφ=Iθcosφ0IURIZ2u
|
Similar Questions
Knowledge Check
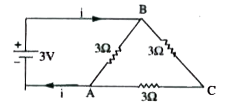
What is the current I in the circuit shown in adjoining Fig. ?
 A2AB1.2AC1AD0.5A
A2AB1.2AC1AD0.5AWhat is the current in the circuit shown below?
 A0ampB10−2ampC1ampD0.10amp
A0ampB10−2ampC1ampD0.10ampThe phase difference between voltage and current in series L-C circuit is
A0∘BπCπ2Dπ3
Find the current in each resistor in the circuit as shown in fig.

View SolutionFind the current in each resistor in the circuit as shown in fig.

View SolutionWhat is the current in the circuit shown below?

View SolutionThe phase difference between voltage and current in series L-C circuit is
View SolutionThe phase difference between voltage and current in an LCR series circuit is
View Solution