Find critical angle for glass and water pair, given refractive index of glass is 1.62 and that of water is 1.33.
To find the critical angle for the glass and water pair, we can use Snell's law, which relates the angles of incidence and refraction to the refractive indices of the two media involved.
1. Identify the Refractive Indices:
- Refractive index of glass (Ng) = 1.62
- Refractive index of water (Nw) = 1.33
2. Understand the Concept of Critical Angle:
The critical angle (θc) is defined as the angle of incidence in the denser medium (glass, in this case) at which the angle of refraction in the less dense medium (water) is 90 degrees.
3. Apply Snell's Law:
According to Snell's law:
Ngsin(θc)=Nwsin(90∘)
Since sin(90∘)=1, we can simplify this to:
Ngsin(θc)=Nw
4. Rearranging the Equation:
We can rearrange the equation to solve for sin(θc):
sin(θc)=NwNg
5. Substituting the Values:
Plugging in the values of the refractive indices:
sin(θc)=1.331.62
6. Calculating sin(θc):
Perform the division:
sin(θc)≈0.82099
7. Finding the Critical Angle:
Now, we take the inverse sine (arcsin) to find the critical angle:
θc=arcsin(0.82099)≈55.18∘
Final Answer:
The critical angle for the glass and water pair is approximately 55.18∘.
- Refractive index of glass (Ng) = 1.62
- Refractive index of water (Nw) = 1.33
The critical angle (θc) is defined as the angle of incidence in the denser medium (glass, in this case) at which the angle of refraction in the less dense medium (water) is 90 degrees.
According to Snell's law:
Ngsin(θc)=Nwsin(90∘)
Since sin(90∘)=1, we can simplify this to:
Ngsin(θc)=Nw
We can rearrange the equation to solve for sin(θc):
sin(θc)=NwNg
Plugging in the values of the refractive indices:
sin(θc)=1.331.62
Perform the division:
sin(θc)≈0.82099
Now, we take the inverse sine (arcsin) to find the critical angle:
θc=arcsin(0.82099)≈55.18∘
The critical angle for the glass and water pair is approximately 55.18∘.
Similar Questions
Knowledge Check
- Question 1 - Select One
The critical angle for glass-air interface is :
A24∘B48∘C42∘D45∘
The critical angle for water is 48.2∘. Find is refractive index.
View SolutionThe refractive index of glass is 1.5. The speed of light in glass is
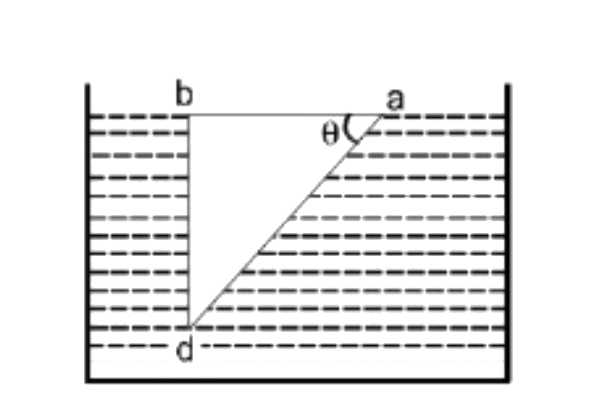
View SolutionA glass prism is immeresed in water as shown in the figure. When a beam of light incident is incident normally on the face ab, it is internally reflected at the face ad. If the refractive index of glass is 1.5 and that of water is 4/3, then
 View Solution
View SolutionIf refractive index of glass is 1.50 and of water is 1.33, then criticle angle is
View SolutionThe optical path of a monochromatic light is same if it goes through 4.0 cm of glass or 4.5 cm of water. If the refractive index of glass is 1.53, the refractive index of the water is
View SolutionA beam of light travelling in water strikes a glass plate, which is also immersed in water. When the angle of incidence is 51∘, the reflected beam is found to be plane polarised . What is the refractive index of glass if the refractive index of water is 43? [tan51∘=1.235]
View SolutionRefractive index of diamond with respect to glass is 1.6 and absolute refractive index of glass is 1.5. Find out the absolute refractive index of diamond.
View Solution

