A uniformly charged and infinitely long line having a linear charge density $' λ'$ is placed at a normal distance $y$ from a point $O$ . Consider a sphere of radius $R$ with $O$ as centre and $R > y$ . Electric flux through the surface of the sphere is

A

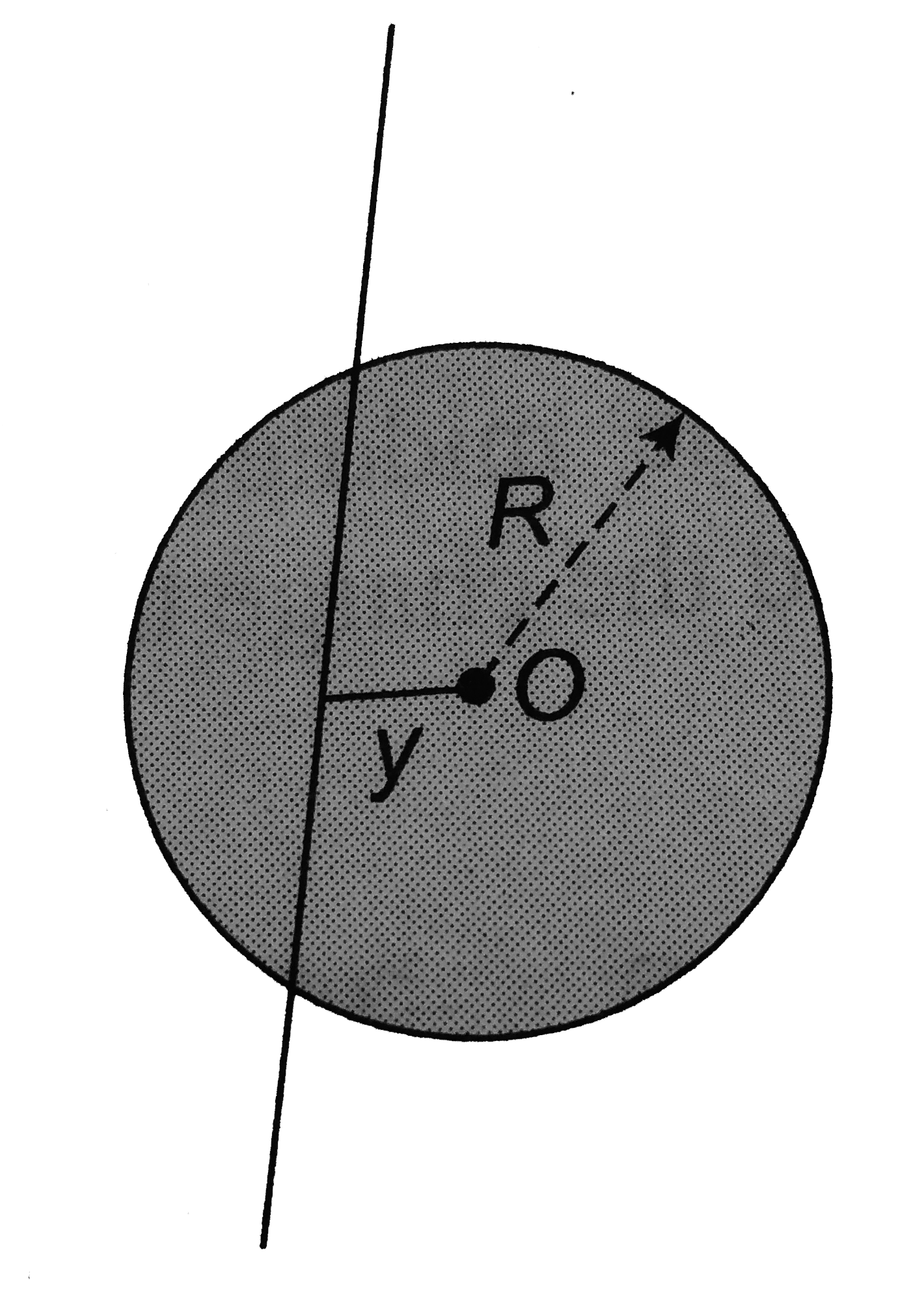
zero

B

$\frac{2 λ R}{ε_{0}}$

C

$\frac{2 λ \sqrt{R^{2} - y^{2}}}{ε_{0}}$

D

$\frac{λ \sqrt{R^{2} + y^{2}}}{ε_{0}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Electric flux $\oint_{s} \to E . - \to d S = \frac{q_{in}}{ε_{0}} q_{in}$ is the charge enclosed by the Gaussian-surface which, in the present case, is the surface of given sphere. As shown, length AB of the line lies inside the sphere.

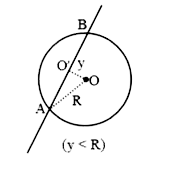
In $Δ O O' A R^{2} = y^{2} + {(O' A)}^{2}$
$∴ O' A = \sqrt{R^{2} - y^{2}}$
and $A B = 2 \sqrt{R^{2} - y^{2}}$
Charge on length $A B = 2 \sqrt{R^{2} - y^{2}} \times λ$
$∴$ electric flux $= \oint_{s} \to E . - \to d S = \frac{2 λ \sqrt{R^{2} - y^{2}}}{ε_{0}}$

|

Updated on:21/07/2023

Class 11 PHYSICS QUIZ

Similar Questions

Knowledge Check

Question 1 - Select One
a point charge $q$ is placed at the centre of a cylinder of length $L$ and radius $R$ the electric flux through the curved surface of the cylinder is
A $\frac{q}{ε_{0}} \frac{L}{\sqrt{L^{2} + R^{2}}}$
B $\frac{q}{ε_{0}} \frac{L}{\sqrt{L^{2} + 2 R^{2}}}$
C $\frac{q}{ε_{0}} \frac{L}{\sqrt{L^{2} + 4 R^{2}}}$
D $\frac{q}{2 ε_{0}}$
Question 2 - Select One
The electric field due to point charged at a distance R form it is E. if the same charge is placed on a metallic sphere of Radius R, the electric field on the surface of the sphere will be
Azero
B10 V
Cmore than
Dnone of these
Question 3 - Select One
A charge $q_{0}$ is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
A $\frac{q_{0}}{4 ε_{0}}$
B $\frac{q_{0}}{2 ε_{0}}$
C $\frac{q_{0}}{3 ε_{0}}$
D $\frac{q_{0}}{ε_{0}}$

Recommended Questions

Home
Ask Doubt
Profile