Use direct method to evaluate :
(ix) (z−23)(z+23)
To evaluate the expression (z−23)(z+23) using the direct method, we can follow these steps:
Step 1: Identify the expression
We start with the expression:
(z−23)(z+23)
Step 2: Apply the distributive property (FOIL method)
Using the distributive property, we multiply each term in the first bracket by each term in the second bracket:
=z⋅z+z⋅23−23⋅z−23⋅23
Step 3: Simplify the terms
Now, we simplify each term:
1. z⋅z=z2
2. z⋅23=2z3
3. −23⋅z=−2z3
4. −23⋅23=−49
Putting these together, we have:
=z2+2z3−2z3−49
Step 4: Combine like terms
Notice that 2z3 and −2z3 cancel each other out:
=z2−49
Final Result
Thus, the evaluated expression is:
z2−49
---
We start with the expression:
(z−23)(z+23)
Using the distributive property, we multiply each term in the first bracket by each term in the second bracket:
=z⋅z+z⋅23−23⋅z−23⋅23
Now, we simplify each term:
1. z⋅z=z2
2. z⋅23=2z3
3. −23⋅z=−2z3
4. −23⋅23=−49
=z2+2z3−2z3−49
Notice that 2z3 and −2z3 cancel each other out:
=z2−49
Thus, the evaluated expression is:
z2−49
Topper's Solved these Questions
- IDENTITIESBOOK - ICSECHAPTER - IDENTITIESEXERCISE - EXERCISE 12(B)
36 Videos
- IDENTITIESBOOK - ICSECHAPTER - IDENTITIESEXERCISE - EXERCISE 12(C)
23 Videos
- IDENTITIESBOOK - ICSECHAPTER - IDENTITIESEXERCISE - EXERCISE 12(D)
49 Videos
- FACTORISATIONBOOK - ICSECHAPTER - FACTORISATIONEXERCISE - EXERCISE 13(F)
49 Videos
- INTEREST (SIMPLE AND COMPOUND)BOOK - ICSECHAPTER - INTEREST (SIMPLE AND COMPOUND)EXERCISE - EXERCISE 9(C)
39 Videos
Similar Questions
Use direct method to evaluate :
(ii) (2+a)(2−a)
View SolutionUse direct method to evaluate :
(xii) (a2−b3)(a2+b3)
View SolutionUse direct method to evaluate :
(v) (2a+3)(2a−3)
View SolutionUse direct method to evaluate :
(x) (35a+12)(35a−12)
View SolutionIf x3+y3+z3=3xyzandx+y+z=0, find the value of :
(x+y)2xy+(y+z)2yz+(z+x)2zx
View SolutionIf z1,z2,z3 are distinct nonzero complex numbers and a,b,c∈R+ such that a|z1−z2|=b|z2−z3|=c|z3−z1| Then find the value of a2z1−z2+b2z2−z3+c2z3−z1
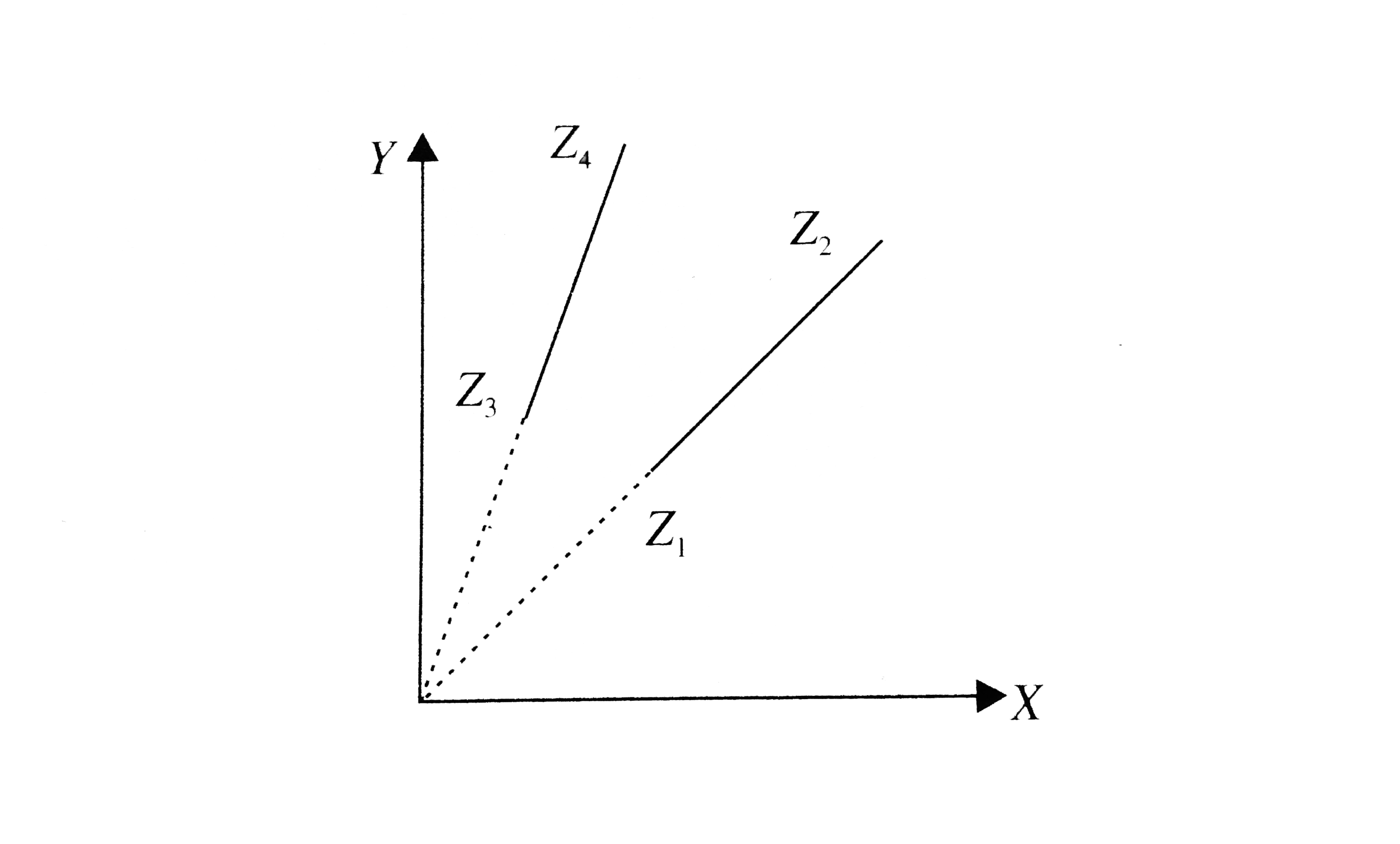
View SolutionIn the diagram as shown, find parameters representing x and y axes and also parameter Z, if Z1=Z2,Z3=Z4 and Z2>Z3:
View SolutionIf x3+y3+z3=3xyz and x+y+z=0, find the value of (x+y)2xy=(y+z)2yz+(z+x)2zx
View SolutionIt is given the complex numbers z1 and z2, |z1|=2 and |z2|=3. If the included angle of their corresponding vectors is 60∘ , then find value of ∣∣∣z1+z2z1−z2∣∣∣
View SolutionComplex numbers z1,z2,z3 are the vertices A,B,C respectively of an isosceles right angled trianglewith right angle at Cand(z1−z2)2=k(z1−z3)(z3−z2), then find k.
View Solution
