If m−1m=5, find : (iii) m2−1m2
To solve the equation m−1m=5 and find m2−1m2, we can follow these steps:
Step 1: Square both sides of the equation
We start with the equation:
m−1m=5
Now, we square both sides:
(m−1m)2=52
This gives us:
m2−2⋅m⋅1m+1m2=25
Simplifying the middle term:
m2−2+1m2=25
Step 2: Rearrange the equation
Now, we rearrange the equation to isolate m2+1m2:
m2+1m2=25+2
This simplifies to:
m2+1m2=27
Step 3: Find m2−1m2
We know that:
m2−1m2=(m−1m)(m+1m)
We already have m−1m=5. Now we need to find m+1m.
Step 4: Find m+1m
Using the identity:
(m−1m)2+4=(m+1m)2
Substituting m−1m=5:
52+4=(m+1m)2
Calculating:
25+4=(m+1m)2
29=(m+1m)2
Taking the square root:
m+1m=√29
Step 5: Substitute back to find m2−1m2
Now we can substitute back into our expression:
m2−1m2=(m−1m)(m+1m)=5⋅√29
Final Answer
Thus, the final answer is:
m2−1m2=5√29
We start with the equation:
m−1m=5
Now, we square both sides:
(m−1m)2=52
This gives us:
m2−2⋅m⋅1m+1m2=25
Simplifying the middle term:
m2−2+1m2=25
Now, we rearrange the equation to isolate m2+1m2:
m2+1m2=25+2
This simplifies to:
m2+1m2=27
We know that:
m2−1m2=(m−1m)(m+1m)
We already have m−1m=5. Now we need to find m+1m.
Using the identity:
(m−1m)2+4=(m+1m)2
Substituting m−1m=5:
52+4=(m+1m)2
Calculating:
25+4=(m+1m)2
29=(m+1m)2
Taking the square root:
m+1m=√29
Now we can substitute back into our expression:
m2−1m2=(m−1m)(m+1m)=5⋅√29
Thus, the final answer is:
m2−1m2=5√29
Topper's Solved these Questions
Similar Questions
Knowledge Check
If m+1=5(m−1)3, then 1m=
A14B38C2D83The nth term of the A.P. −1m,1+mm,1+2mm,... is :
A1+nmB1+m(n+1)mC1+mnmD1+m(n−1)mLet P(n)=1+3+5+...+(2n−1)=3+n2, then which of the following is true?
(i) P (3) is correct
(ii) P (2) is correct
(iii) P(m)⇒p(m+1)
(iv) P(m) cancel(rArr) P(m+1)AP (3) is correctBP (2) is correctCP(m)⇒p(m+1)DP(m) cancel(rArr) P(m+1)
If l : m = 212:123 and m : n = 114:312 , find l : m : n
View SolutionIf m=2 find the value of : (i) m−2 (ii) 3m−5 (iii) 9−5m (iv) 3m2−2m−7
View SolutionIn the given diagram , find the relation between acceleration of blocks m1andm2 . (m2 remains horizontal ).
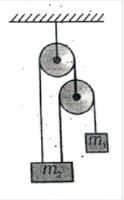
View SolutionIf 2−m ×12m=14, then 114 {(4m)1/2+ (15m)−1} is equal to
(a)12
(b) 2
(c) 4
(d) −14
View SolutionFind (m+n)÷(m−n), if :
(i) m=23andn=32
(ii) m=34andn=43
(iii) m=45andn=−310
View Solution
