Given below are the angles x and y.

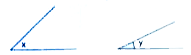
Without measuring these angles, construct:
(i) $∠ A B C = x + y$
(ii) $∠ A B C = 2 x + y$
(iii) $∠ A B C = x + 2 y$ .

Video Solution

|

Answer

Step by step video & image solution for Given below are the angles x and y. Without measuring these angles, construct: (i) angleABC=x+y (ii) angleABC=2x+y (iii) angleABC=x+2y. by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.

Updated on:21/07/2023

Class 8 MATHS PRACTICAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
From the following figure, find
$(i) x$
$(i i)$ $∠ A B C$
$(i i i)$ $∠ A C D$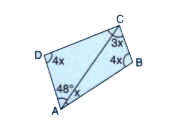
A $(i)$ $x = 18^{\circ}$
$(i i) ∠ A B C = 124^{\circ}$
$(i i i)$ $∠ A C D = 30^{\circ}$
B $(i)$ $x = 16^{\circ}$
$(i i) ∠ A B C = 104^{\circ}$
$(i i i)$ $∠ A C D = 28^{\circ}$
C $(i)$ $x = 26^{\circ}$
$(i i) ∠ A B C = 114^{\circ}$
$(i i i)$ $∠ A C D = 36^{\circ}$
D $(i)$ $x = 26^{\circ}$
$(i i) ∠ A B C = 104^{\circ}$
$(i i i)$ $∠ A C D = 28^{\circ}$

ICSE-CONSTRUCTION (USING RULER AND COMPASSES ONLY)-EXERCISE 18(A)

Home
Ask Doubt
Profile