If P = { letters of MUMBAI } and Q = { letters of CHENNAI } , then represent the following sets by Venn diagrams .
(i) P (ii)Q (iii) P∪Q (iv) P∩Q
To solve the problem, we will follow these steps to represent the sets P and Q using Venn diagrams, and also find their union (P ∪ Q) and intersection (P ∩ Q).
Step 1: Identify the elements of sets P and Q
- Set P: The letters of "MUMBAI" are {M, U, M, B, A, I}. Since we only consider unique elements, we have:
- P = {M, U, B, A, I}
- Set Q: The letters of "CHENNAI" are {C, H, E, N, N, A, I}. Again, considering unique elements:
- Q = {C, H, E, N, A, I}
Step 2: Draw the Venn Diagram
- Draw two overlapping circles. Label one circle as Set P and the other as Set Q.
Step 3: Fill in the elements of Set P
- In Circle P, write the unique elements of Set P:
- P = {M, U, B, A, I}
- Place A and I in the overlapping area since they will also be part of the intersection.
Step 4: Fill in the elements of Set Q
- In Circle Q, write the unique elements of Set Q:
- Q = {C, H, E, N, A, I}
- Place A and I in the overlapping area as they are common to both sets.
Step 5: Identify the union of sets P and Q (P ∪ Q)
- The union of two sets includes all unique elements from both sets:
- P ∪ Q = {M, U, B, A, I, C, H, E, N}
Step 6: Identify the intersection of sets P and Q (P ∩ Q)
- The intersection of two sets includes only the elements that are common to both sets:
- P ∩ Q = {A, I}
Final Representation in the Venn Diagram
- The final Venn diagram will show:
- Circle P containing M, U, B, A, I (with A and I in the overlapping area)
- Circle Q containing C, H, E, N, A, I (with A and I in the overlapping area)
- The overlapping area (intersection) will contain A and I.
Summary of the Sets
- P = {M, U, B, A, I}
- Q = {C, H, E, N, A, I}
- P ∪ Q = {M, U, B, A, I, C, H, E, N}
- P ∩ Q = {A, I}
---
- Set P: The letters of "MUMBAI" are {M, U, M, B, A, I}. Since we only consider unique elements, we have:
- P = {M, U, B, A, I}
- Set Q: The letters of "CHENNAI" are {C, H, E, N, N, A, I}. Again, considering unique elements:
- Q = {C, H, E, N, A, I}
- Draw two overlapping circles. Label one circle as Set P and the other as Set Q.
- In Circle P, write the unique elements of Set P:
- P = {M, U, B, A, I}
- Place A and I in the overlapping area since they will also be part of the intersection.
- In Circle Q, write the unique elements of Set Q:
- Q = {C, H, E, N, A, I}
- Place A and I in the overlapping area as they are common to both sets.
- The union of two sets includes all unique elements from both sets:
- P ∪ Q = {M, U, B, A, I, C, H, E, N}
Step 6: Identify the intersection of sets P and Q (P ∩ Q)
- The intersection of two sets includes only the elements that are common to both sets:
- P ∩ Q = {A, I}
- The final Venn diagram will show:
- Circle P containing M, U, B, A, I (with A and I in the overlapping area)
- Circle Q containing C, H, E, N, A, I (with A and I in the overlapping area)
- The overlapping area (intersection) will contain A and I.
- P = {M, U, B, A, I}
- Q = {C, H, E, N, A, I}
- P ∪ Q = {M, U, B, A, I, C, H, E, N}
- P ∩ Q = {A, I}
Similar Questions
Knowledge Check
In an AP the pth term is q and the (p+q)th term is zero, then the qth term is (i) −p (ii) p (iii) p+q (iv) p−q
A−pBpCp+qDp−q
Represent the following sets by Venn diagrams :
Q = { vowels in the word NUMERICAL}
View SolutionRepresent the following sets by Venn diagrams :
P = { letters in the word TEMPERATURE }
View SolutionIf P = { natural numbers upto 10 } and Q = {3,6,9} , find P∪Q,P∩Q represent these by Venn diagrams .
View SolutionFrom the adjoining Venn diagram , find the following sets :
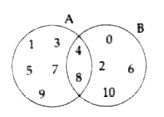
(i) A (ii) B (III) A∪B (iv) A∩B
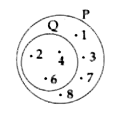
View SolutionFrom the adjoining Venn diagram , find the following sets :
P∪Q
View SolutionThe diagram, given below, represents two inequations P and Q on real number lines :

Represent each of the following sets on different number lines :
(a) P∪Q
(b) P∩Q
(c ) P−Q
(d) Q - P
(e ) P∩Q
(f) P∩Q
View SolutionIf P {x : x is a letter in the word CHANDIGARH } and Q = {x : x is a letter in the word JAMNAGAR }, then
find n(P) , n(Q) n(P∪Q)andn(P∩Q)
View Solution