Simplify the following
(t−2)(t+3)
To simplify the expression (t−2)(t+3), we will use the distributive property (also known as the FOIL method for binomials). Here are the steps:
Step 1: Distribute t from the first binomial to both terms in the second binomial.
t⋅(t+3)=t⋅t+t⋅3=t2+3t
Step 2: Distribute −2 from the first binomial to both terms in the second binomial.
−2⋅(t+3)=−2⋅t+(−2)⋅3=−2t−6
Step 3: Combine the results from Step 1 and Step 2.
Now we combine the expressions we obtained:
t2+3t−2t−6
Step 4: Combine like terms.
Combine 3t and −2t:
t2+(3t−2t)−6=t2+1t−6
Final Answer:
Thus, the simplified expression is:
t2+t−6
---
t⋅(t+3)=t⋅t+t⋅3=t2+3t
−2⋅(t+3)=−2⋅t+(−2)⋅3=−2t−6
Now we combine the expressions we obtained:
t2+3t−2t−6
Combine 3t and −2t:
t2+(3t−2t)−6=t2+1t−6
Thus, the simplified expression is:
t2+t−6
Similar Questions
Simplify the following: (2i)3
View SolutionEvaluate/simplify the following: |23−34|
View SolutionSimplify each of the following expressions: 4st (s−t)−6s2(t−t2)−3t2(2s2−s)+2st(s−t)
View SolutionWhich of the following points lie on the parabola x2=4ay? a.x=at2,y=2at b. x=2at, y=at2 c. x=2at2,y=at d. x=2at, y=at2
View SolutionThe displacement s of an object is given as a function of time t by the following equation s=2t+5t2+3t3. Calculate the instantaneous velocity of the object at t = 1 s.
View SolutionSolve the following equation: tanθ+tan2θ+tan3θ=0
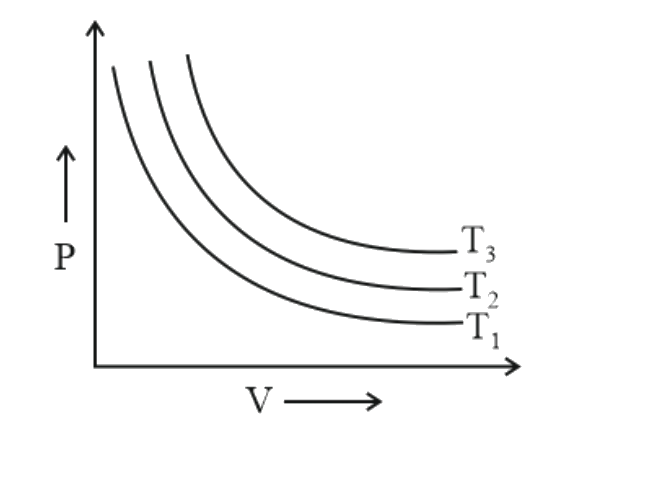
View Solutionfor the given PV isotherms , which of the following is correct for T1,T2,T3 ?
View SolutionThe velocity of an object is changing with time and relation is given by the following equation.
v=2t+3t2
Calculate the position of the object from the origin at t = 2 s.
Assume particle to be at origin at t = 0
View SolutionWhich among the following relations is correct?
(a)t3/4=2t1/2
(b)t3/4=3t1/2
(c)t3/4=12t1/2
(d)t3/4=13t1/2
View SolutionA particle moves in x-y plane and at time t is at the point (t2,t3−2t), then which of the following is/are correct?
View Solution
