On adding −17ab,−5aband13ab , we get
−9ab
9ab
−12ab
none of these
To solve the problem of adding −17ab, −5ab, and 13ab, we can follow these steps:
Step 1: Write down the expression
We start with the expression:
−17ab+(−5ab)+13ab
Step 2: Combine the negative terms
First, we add the negative terms together:
−17ab−5ab=−22ab
Step 3: Add the positive term
Now, we add the positive term 13ab to the result from Step 2:
−22ab+13ab
Step 4: Combine the terms
Now, we combine −22ab and 13ab:
−22ab+13ab=−9ab
Final Answer
Thus, the final result of adding −17ab, −5ab, and 13ab is:
−9ab
---
We start with the expression:
−17ab+(−5ab)+13ab
First, we add the negative terms together:
−17ab−5ab=−22ab
Now, we add the positive term 13ab to the result from Step 2:
−22ab+13ab
Now, we combine −22ab and 13ab:
−22ab+13ab=−9ab
Thus, the final result of adding −17ab, −5ab, and 13ab is:
−9ab
Similar Questions
Knowledge Check
In the figure, if AB=8,BC=6,AC=10andCD=9, then AD =
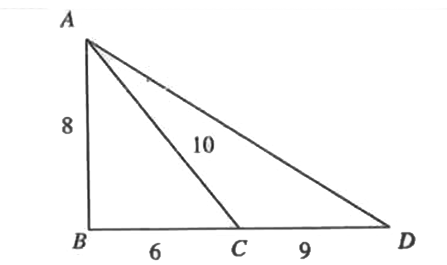 A12B13C15D17
A12B13C15D17
Using column method , add ab+2bc−caand2ab−bc−ca and subtract 4ab+5bc−3ca
View SolutionIn ΔABC,AB=BC,AD⊥BCandCE⊥AB, prove that AD = CE.
View SolutionMultiply :
3a2b−5ab by 3ab
View SolutionAdd the following: 4ab–5bc+7ca,–3ab+2bc–3ca,5ab–3bc+4ca
View SolutionMatrix A ha s m rows and n+ 5 columns; matrix B has m rows and 11−n columns. If both AB and BA exist, then (A) AB and BA are square matrix (B) AB and BA are of order 8×8 and 3×13, respectively (C) AB=BA (D) None of these
View SolutionAdd :
13ab−9cd−xy,5xy,15cd−7ab,6xy−3cd
View SolutionIn the following figure , AB = BC , AD ⊥BCandCE⊥AB.prove that AD = CE
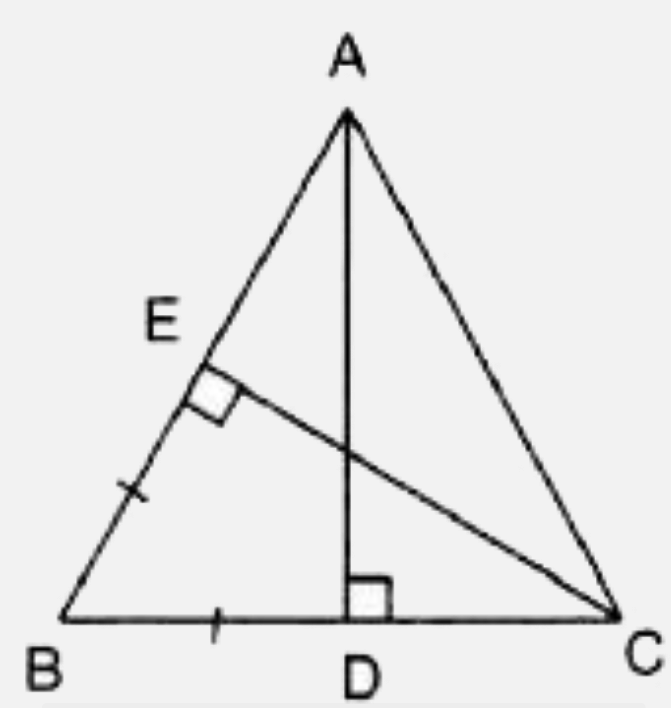
View Solution
