The vector −2ˆi+4ˆj+4ˆkand−4ˆi−4ˆk represent the diagonals BD and AC of a parallelogram ABCD. Then, find the area of the parallelogram.
The correct Answer is:12∣∣→d1×→d2∣∣ where →d1and→d2 are the diagonal vectors.
To find the area of the parallelogram ABCD given the diagonals BD and AC represented by the vectors −2^i+4^j+4^k and −4^i+0^j−4^k, we can follow these steps:
Step 1: Identify the Diagonal Vectors
Let:
- d1=−2^i+4^j+4^k (Diagonal AC)
- d2=−4^i+0^j−4^k (Diagonal BD)
Step 2: Calculate the Cross Product d1×d2
To find the area of the parallelogram, we need to calculate the cross product of the two diagonal vectors. The area A of the parallelogram is given by:
A=12|d1×d2|
The cross product can be calculated using the determinant of a matrix:
d1×d2=∣∣
∣
∣∣^i^j^k−244−40−4∣∣
∣
∣∣
Step 3: Calculate the Determinant
Expanding the determinant:
d1×d2=^i∣∣∣440−4∣∣∣−^j∣∣∣−24−4−4∣∣∣+^k∣∣∣−24−40∣∣∣
Calculating each of these 2x2 determinants:
1. For ^i:
4⋅(−4)−4⋅0=−16
2. For −^j:
−((−2)⋅(−4)−4⋅(−4))=−(8+16)=−24
3. For ^k:
(−2)⋅0−4⋅(−4)=0+16=16
Putting it all together:
d1×d2=−16^i+24^j+16^k
Step 4: Calculate the Magnitude of the Cross Product
Now we find the magnitude of the cross product:
|d1×d2|=√(−16)2+(24)2+(16)2
Calculating each term:
- (−16)2=256
- 242=576
- 162=256
Adding these:
|d1×d2|=√256+576+256=√1088
Step 5: Simplify the Magnitude
We can simplify √1088:
√1088=√64×17=8√17
Step 6: Calculate the Area of the Parallelogram
Finally, we can find the area of the parallelogram:
A=12|d1×d2|=12×8√17=4√17
Thus, the area of the parallelogram ABCD is:
4√17 square units
Let:
- d1=−2^i+4^j+4^k (Diagonal AC)
- d2=−4^i+0^j−4^k (Diagonal BD)
To find the area of the parallelogram, we need to calculate the cross product of the two diagonal vectors. The area A of the parallelogram is given by:
∣
∣∣^i^j^k−244−40−4∣∣
∣
∣∣
Expanding the determinant:
4⋅(−4)−4⋅0=−16
−((−2)⋅(−4)−4⋅(−4))=−(8+16)=−24
(−2)⋅0−4⋅(−4)=0+16=16
Now we find the magnitude of the cross product:
- 242=576
- 162=256
We can simplify √1088:
Finally, we can find the area of the parallelogram:
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 04EXERCISE - SECTION .C.12videos
SELF ASSESSMENT PAPER 04
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 04EXERCISE - SECTION .C.12videos
SELF ASSESSMENT PAPER 04
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 03EXERCISE - Section -C10videos
SELF ASSESSMENT PAPER 03
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 05EXERCISE - SECTION .C.12videos
SELF ASSESSMENT PAPER 05
Similar Questions
Show that the vectors 2ˆi−3ˆj+4ˆk and −4ˆi+6ˆj−8ˆk are collinear.
View SolutionGiven two vectors →a=−ˆi+ˆj+2ˆkand→b=−ˆi−2ˆj−ˆk
Find
a. →a×→b then use this to find the area of the triangle.
b. The area of the parallelogram
c. The area of a paralleogram whose diagonals are
2 veca and 4vecbView SolutionLet ¯¯¯¯¯¯PR=3ˆi+ˆj−2ˆkand¯¯¯¯¯¯SQ=ˆi−3ˆj−4ˆk determine diagonals of a parallelogram PQRS and ¯¯¯¯¯¯PT=ˆi+2ˆj+3ˆk be another vector. Then the volume of the parallelepiped determined by the vectors ¯¯¯¯¯¯PT,¯¯¯¯¯¯PQand¯¯¯¯¯PS is
View SolutionIf a=2ˆi+3ˆj+4ˆkandb=4ˆi+3ˆj+2ˆk ,find the angel between a and b.
View SolutionIf in the shown figure AC=ˆi+2ˆj+4ˆk and BD=ˆi−3ˆj+ˆk then BC is
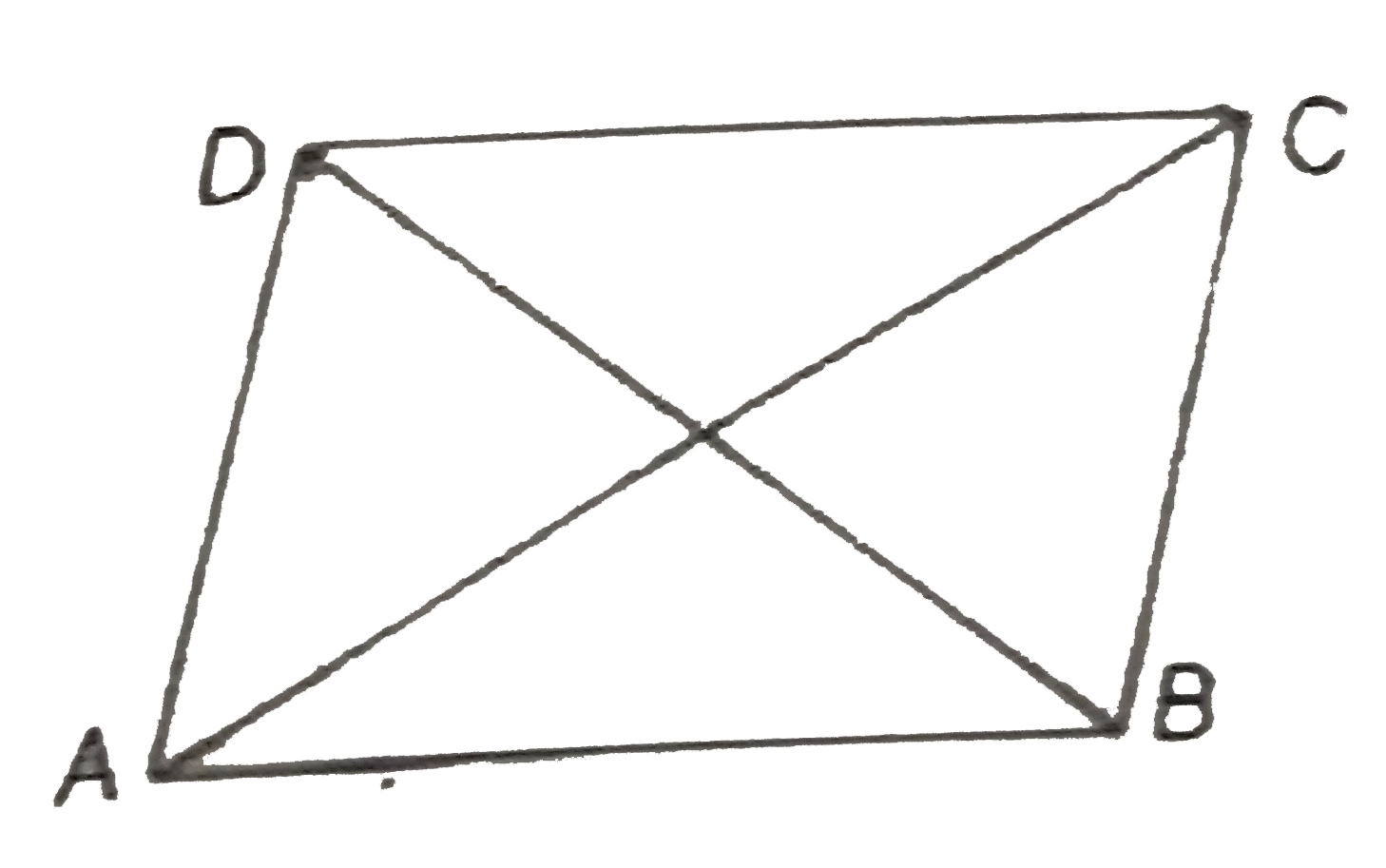 View Solution
View SolutionShow that the vectors ˆi−ˆj−ˆk,2ˆi+3ˆj+ˆkand7ˆi+3ˆj−4ˆk are coplanar.
View SolutionThe position vectors of the point A,B,CandD are 3ˆi−2ˆj−ˆk,2ˆi+3ˆj−4ˆk,−ˆi+ˆj+2ˆkand4ˆi+5ˆj+λˆk, respectively. If the points A, B, C and D lie on a plane, find the value of λ.
View SolutionVectors along the adjacent sides of parallelogram are →a=2ˆi+4ˆj−5ˆkand→b=ˆi+2ˆj+3ˆk. Find the length of the longer diagonal of the parallelogram.
View SolutionThe sides of a parallelogram are 2ˆi+4ˆj−5ˆkandˆi+2ˆj+3ˆk. The unit vector parallel to one of the diagonals is
View SolutionVectors along the adjacent sides of parallelogram are →a=ˆi+2ˆj+ˆkand→b=2ˆi+4ˆj+ˆk. Find the length of the longer diagonal of the parallelogram.
View Solution

