Spin angular momentum of an electron has no analog in classical mechanics. however, it turns out that the treatment is closely analogous to the treatment of orbital angular momentum. Spin angular momentum=√s(s+1)h2π, Orbital angular momentum = (l(l+1))h2π-Which of the following electronic configuration have zero spin quantum number?Solution in Bengali
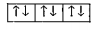
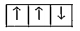
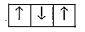

The correct Answer is:1
Step by step video, text & image solution for Spin angular momentum of an electron has no analog in classical mechanics. however, it turns out that the treatment is closely analogous to the treatment of orbital angular momentum. Spin angular momentum=sqrt(s(s+1))h/(2pi), Orbital angular momentum = (l(l+1))h/(2pi)-Which of the following electronic configuration have zero spin quantum number? by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
State the number of significant figures in the following
62.401:29View SolutionSpin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum Spin angular momentum =sqrt(s(s+1))h Orbital angular momentum =sqrt(l(l+1))h Total spin of ana tom or ion is a multiple of (1)/(2) . Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion. Spin multiplicity =(2sums+1) Q. Total spin of Mn^(2+)(Z=25) ion will be:
02:20View SolutionSpin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum =√s(s+1)h
Orbital angular momentum=√l(l+1)h
Total spin of ana tom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity =(2∑s+1)
Q. Which of the following electronic configurations have four spin multiplicity?02:38View SolutionSpin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum =√s(s+1)h
Orbital angular momentum=√l(l+1)h
Total spin of ana tom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity =(2∑s+1)
Q. Which of the following quantum numbers is not derived from schrodinger wave equations?03:12View SolutionSpin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum Spin angular momentum =sqrt(s(s+1))h Orbital angular momentum =sqrt(l(l+1))h Total spin of ana tom or ion is a multiple of (1)/(2) . Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion. Spin multiplicity =(2sums+1) Q. In any subshell, the maximum number of electrons having same value of spin quantum numbers is:
01:33View SolutionSpin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum Spin angular momentum =sqrt(s(s+1))h Orbital angular momentum =sqrt(l(l+1))h Total spin of ana tom or ion is a multiple of (1)/(2) . Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion. Spin multiplicity =(2sums+1) Q. The orbital angular momentum of a 2p-electron is:
02:45View SolutionThe ratio of orbital angular momentum and spin angular momentum of an electron in 'p' orbital is
01:50View Solutionएक कक्षा में चक्कर लगा रहे इलेक्ट्रॉन का कक्षकीय कोणीय संवेग ( orbital angular momentum ) h2π√l(l+1) है । s-इलेक्ट्रॉन के लिए इसका संवेग है :
03:44View Solutionकिसी कक्ष में गति करते हुए इलेक्ट्रॉन का कोणीय संवेग निम्न व्यंजक द्वारा दिया जाता है : √l(l+1).h2π अतः एक s-इलेक्ट्रॉन का संवेग होगा-
View SolutionThe orbital angular momentum for an electron revolving in an orbit is given by √l(l+1)h2π. This momentum for an s-electron will be given by
01:23View Solutionগৌণ কোয়ান্টাম সংখ্যা l-এর জন্য কোনো অর্বিট্যালে ইলেকট্রনের কৌণিক ভরবেগ √l(l+1)h2π হলে s -অর্বিট্যালে ইলেকট্রনের কৌণিক ভরবেগের মান -
00:49View SolutionThe orbital angular momentum for an electron revolving in an orbit is given by √l(l+1)h2π. What is the momentum of an s-electron?
03:21View Solutionएक कक्षक में एक घूमते हुए इलेक्ट्रॉन का कक्षक कोणीय संवेग √l(l+1).h2π है। s-इलेक्ट्रॉन के लिए संवेग का मान होगा
03:03View SolutionSpin angular momentum of an electron has no analog in classical mechanics. However, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum.
Spin angular momentum =√s(s+1)h
Orbital angular momentum =√l(l+1)h
Total spin of an atom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity (2∑s+1)
Total spin of Mn2+ = (Z = 25) ion will be :11:54View SolutionSpin angular momentum of an electron has no analog in classical mechanics. However, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum. Spin angular momentum = sqrt(s(s+1)h) Orbital angular momentum = sqrt(l(l+1)h) Total spin of an atom or ion is a multiple of (1)/(2) . Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion. Spin multiplicity (2 sum s +1) In any subshell, the maximum number of electrons having same value of spin quantum number is :
04:06View SolutionSpin angular momentum of an electron has no analog in classical mechanics. However, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum. Spin angular momentum = sqrt(s(s+1)h) Orbital angular momentum = sqrt(l(l+1)h) Total spin of an atom or ion is a multiple of (1)/(2) . Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion. Spin multiplicity (2 sum s +1) The orbital angular momentum for a 2p-electron is :
02:17View Solution

