In △ABC two points L and M are taken in the sides AB and AC such that LM∣∣BC and BL=x-3,AB=2x,CM=x-2,AC=2x+3 then find the value of x.Solution in Assamese
Step by step video & image solution for In triangleABC two points L and M are taken in the sides AB and AC such that LM|\|BC and BL=x-3,AB=2x,CM=x-2,AC=2x+3 then find the value of x. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
All circles are ______ . (congruent, similar)
View Solution2 cubes each of volume 64cm3 are joined end to end.Find the surface area of the resulting cuboid.
View SolutionX and Y are points on the sides AB and BC respectively of △ABC such that XY||AC and XY divides △ABC into two parts in area , find AXAB
View Solutionयदि AB=x+3,BC=2x और AC=4x−5, तब x के किस मान के लिए B, AC पर स्थित है ?
View Solutionचित्र में LM∣∣AB दिया है| यदि AL=x−3,AC=2x,BM=x−2, तथा BC=2x+3 हो तो x का मान ज्ञात करें|
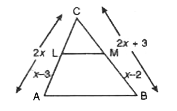
View SolutionIn the adjoining figure, LM∣∣AB and if AL=(x−3) unit, AC=2x unit. BM=(x−2) unit and BC=(2x+3) unit, find the value of x.
View SolutionIn the given figure , LM∣∣AB AL=x-3, AC=2x,BM=x-2 and BC=2x+3, find the value of x.
View Solutionఇచ్చిన పటంలోLM∣∣AB AL=x-3, AC =2x, BM=x-2 మరియు BC=2x+3 అయిన x విలువను కనుగొనుము.
View SolutionIn the given figure LM||AB M
AL = x - 3, AC = 2x, BM = x - 2
and BC = 2x + 3 find the value of x
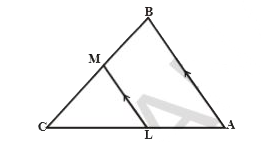
View SolutionIn the given figure LM||AB M
AL = x - 3, AC = 2x, BM = x - 2
and BC = 2x + 3 find the value of x
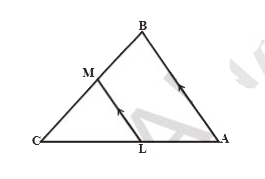
View SolutionIn the given figure LM||AB M
AL = x - 3, AC = 2x, BM = x - 2
and BC = 2x + 3 find the value of x
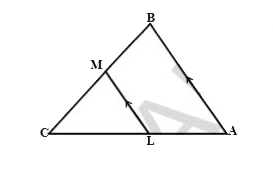
View Solutionপাশের চিত্রে, LM∣∣AB এবং AL = ( x-3 ) একক, AC = 2x একক, BM = ( x-2 ) একক এবং BC = ( 2x+3 ) একক হলে, x -এর মান নির্ণয় করো ।
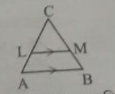
View SolutionIn Figure, LM∣∣AB If AL=x−3, AC=2x, BM=x−2 and BC=2x+3 , find the value of x .
View Solutionदी गई आकृति में, LM ∣∣ AB | यदि AL = x-3, AC = 2x, BM = x-2, BC = 2x+ 3 हों , तो x का मान ज्ञात कीजिए।
View SolutionIn △ABC,∠B=90∘. Find the sides of the triangle if:
AB=(x−3)cm,BC=(x+4)cm and AC=(x+6)cm.
View Solution
