In FIg. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB=AC. If AD⊥BC and EF⊥AC, prove that △ABD~△ECF.
 Solution in Assamese
Solution in Assamese
Step by step video & image solution for In FIg. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB=AC. If AD_|_BC and EF_|_AC, prove that triangleABD~triangleECF. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
All circles are ______ . (congruent, similar)
View Solution2 cubes each of volume 64cm3 are joined end to end.Find the surface area of the resulting cuboid.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn Fig, find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_032_Q01.png" width="80%"gt
View SolutionAt point P, the value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_025_Q01.png" width="80%"gt
View SolutionIn Fig E is a point on side CB produced of an isosceles triangle ABC with AB=AC. If AD⊥BCandEF⊥AC , prove that ΔABD~ΔECT
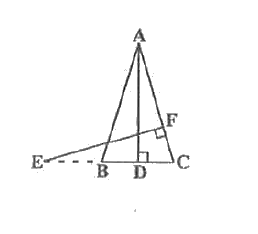
View Solution
