P and Q are respectively the base and the vertex of the tower PQ.AB is another tower which is at a certain distance apart from PQ.The height of AB is less than that of PQ and the base of AB is A.The angles of elevation of Q from A and B are respectively 60∘ and 45∘.If AB=40m,find PQ,QA and QB.Solution in Assamese
Step by step video & image solution for P and Q are respectively the base and the vertex of the tower PQ.AB is another tower which is at a certain distance apart from PQ.The height of AB is less than that of PQ and the base of AB is A.The angles of elevation of Q from A and B are respectively 60^@ and 45^@.If AB=40m,find PQ,QA and QB. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
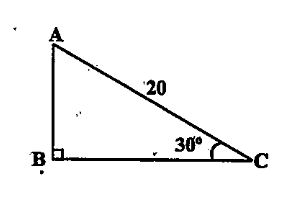
A circus artist is climbing a 20 m long rope.which is tightly stretched and tied from the top of a vertical pole to the ground.Find the height of the pole,if the angle made by the rope with the ground level is 30∘(see Fig 9.11)
View SolutionWhich of the following ratios are in proportion? 12 : 21 and 32 : 56
View SolutionWhat is the median of the data 15,8,10,6,12,11,4,7,3?
View SolutionThe angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60^(@). From a point y40m vertically above X, the angle of elevation the top Q of tower is 45^(@). Find the height of the tower PQ and the distance PX.(Use sqrt(3)=1.73)
View SolutionPQ is a post of height a,AB is a tower of height h at a distance x from the post,and alpha and beta are the angles of elevation of B, at P and Q respectively such that alpha
View SolutionPQ is a post of given height a , and AB is a tower at some distance. If α and β are the angles of elevation of B , the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
View SolutionThe angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60∘. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45∘. Find the height of the tower PQ and the distance PX. (Use √3=1.73).
View Solutionकिसी मीनार के आधार से a और b दूरी पर एक ही रेखा में स्थित दो बिंदुओं P और Q से मीनार के शिखर के उन्नयन कोण एक –दूसरे एक कोटिपूरक पाये जाते हैं। सिद्ध कीजिए कि मीनार की ऊंचाई √ab के बराबर होगी। यदि a=18 मीटर तथा b=32 मीटर हो तो मीनार की ऊंचाई कितनी होगी?
(अथवा) किसी मीनार के आधार से a और b दूरी पर एक ही सरल रेखा में स्थित दो बिंदुओं PऔरQ से देखने पर मीनार के ऊपरी सिरे के उन्नयन कोण कोटिपूरक है। सिद्ध कीजिए कि मीनार की ऊंचाई √ab है।
View Solutionएक मीनार के शिखर के उन्नयन कोण, दो बिन्दुओं A तथा B जो एक ही रेखा में मीनार के आधार से क्रमश: p तथा q दूरी पर हैं, से क्रमश: 306(∘) तथा 60∘ हैं तो सिद्ध कीजिए कि मीनार की ऊँचाई √pq है।
View Solutionएक खंभा PQ=a से कुछ दूरी पर एक मीनार AB है | यदि P तथा Q से मीनार के शीर्ष B के उन्नयन कोण क्रमशः α तथा βहैं , तो मीनार की ऊँचाई तथा खंभे से इसकी दूरी ज्ञात कीजिए |
View Solutionकिसी मीनार के आधार से गुजरनेवाली सरल रेखा पर a और b दूरियाँ पर स्तिथ क्रमश: दो बिंदुओं P और Q से मीनार के शीर्ष के उन्नयन कोण पूरक है| सिद्ध कीजिये की मीनार की ऊँचाई √ab है|
View Solutionएक मीनार के आधार से 60मीकिदूरीपरएकबिंदुसेमीनारकेशिखरकाउन्नयनकोण45^(@) है तो मीनार कि ऊंचाई है -
View SolutionThe angle of elevation of the top Q of a vertical tower PQ from a point X and the ground is 60∘. From a point Y, 40m vertically above X, the angle of elevation of the top Q of the tower is 45∘. Find the height of the tower PQ and the distance PX. (use √3 = 1.73).
View SolutionThe angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60∘.From a point y 40 m vertically above X, the angle of elevation the top Q of tower is 45∘.Find the height of the tower PQ and the distance PX.(Use √3=1.73)
View SolutionThe angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60∘.From a point y 40 m vertically above X, the angle of elevation the top Q of tower is 45∘.Find the height of the tower PQ and the distance PX.(Use √3=1.73)
View Solution
