Let A1,A2 and A3 be the region on R2 defined by A1={(x,y):x≥0,y≥0,2x+2y−x2−y2>1>x+y},A2={(x,y):x≥0,y≥0,x+y>1>x2+y2},A3={(x,y):x≥0,y≥0,x+y>1>x3+y3}. Denote by |A1|,|A2|, and |A3| respectively. Then
|A1|>|A2|>|A3|
|A1|>|A3|>|A2|
|A1|=|A2|>|A3|
|A1|=|A3|>|A2|
To solve the problem, we need to analyze the regions A1, A2, and A3 defined in R2 and find the areas |A1|, |A2|, and |A3|.
Step 1: Analyze Region A1
The region A1 is defined by the inequalities:
1. 2x+2y−x2−y2>1
2. x+y<1
3. x≥0
4. y≥0
We can rewrite the first inequality:
x2+y2−2x−2y<−1
Completing the square:
(x−1)2+(y−1)2<2
This describes a circle centered at (1,1) with radius √2.
The second inequality x+y<1 describes a line that intersects the x-axis at (1,0) and the y-axis at (0,1).
Step 2: Find the Area of Region A1
To find the area of A1, we need to find the area of the quarter circle (since x and y are non-negative) that lies below the line x+y=1.
The area of the quarter circle is:
Area of quarter circle=14πr2=14π(2)=π2
Now, we need to subtract the area of the triangle formed by the points (0,0), (1,0), and (0,1):
Area of triangle=12×base×height=12×1×1=12
Thus, the area |A1| is:
|A1|=π2−12
Step 3: Analyze Region A2
The region A2 is defined by:
1. x+y>1
2. x2+y2<1
3. x≥0
4. y≥0
The second inequality describes a circle centered at the origin with radius 1. The first inequality describes the area above the line x+y=1.
Step 4: Find the Area of Region A2
The area of the quarter circle is:
Area of quarter circle=14π(12)=π4
The area above the line x+y=1 in the quarter circle can be found similarly to A1. The area of the triangle formed by the points (0,0), (1,0), and (0,1) is:
Area of triangle=12
Thus, the area |A2| is:
|A2|=π4−12
Step 5: Analyze Region A3
The region A3 is defined by:
1. x+y>1
2. x3+y3<1
3. x≥0
4. y≥0
The analysis of A3 follows a similar pattern, but the curve x3+y3=1 is less steep than the circle, and thus the area will be larger than that of A2.
Conclusion
From the analysis:
- |A1|=π2−12
- |A2|=π4−12
- |A3|>|A2|
Thus, we conclude:
|A1|=|A2|<|A3|
1. 2x+2y−x2−y2>1
2. x+y<1
3. x≥0
4. y≥0
x2+y2−2x−2y<−1
Completing the square:
(x−1)2+(y−1)2<2
This describes a circle centered at (1,1) with radius √2.
Area of quarter circle=14πr2=14π(2)=π2
Area of triangle=12×base×height=12×1×1=12
|A1|=π2−12
1. x+y>1
2. x2+y2<1
3. x≥0
4. y≥0
Area of quarter circle=14π(12)=π4
Area of triangle=12
|A2|=π4−12
1. x+y>1
2. x3+y3<1
3. x≥0
4. y≥0
- |A1|=π2−12
- |A2|=π4−12
- |A3|>|A2|
|A1|=|A2|<|A3|
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The region in the xy plane given by y−x≤1,2x−6y≤3,x≥0,y≥0 is
AboundedBnot convexCunbounded convexDbounded and convex - Question 2 - Select One
Shaded, region of the constraints 4x+3y≤12,−x+y≤2,x≥0,y≥0 is
A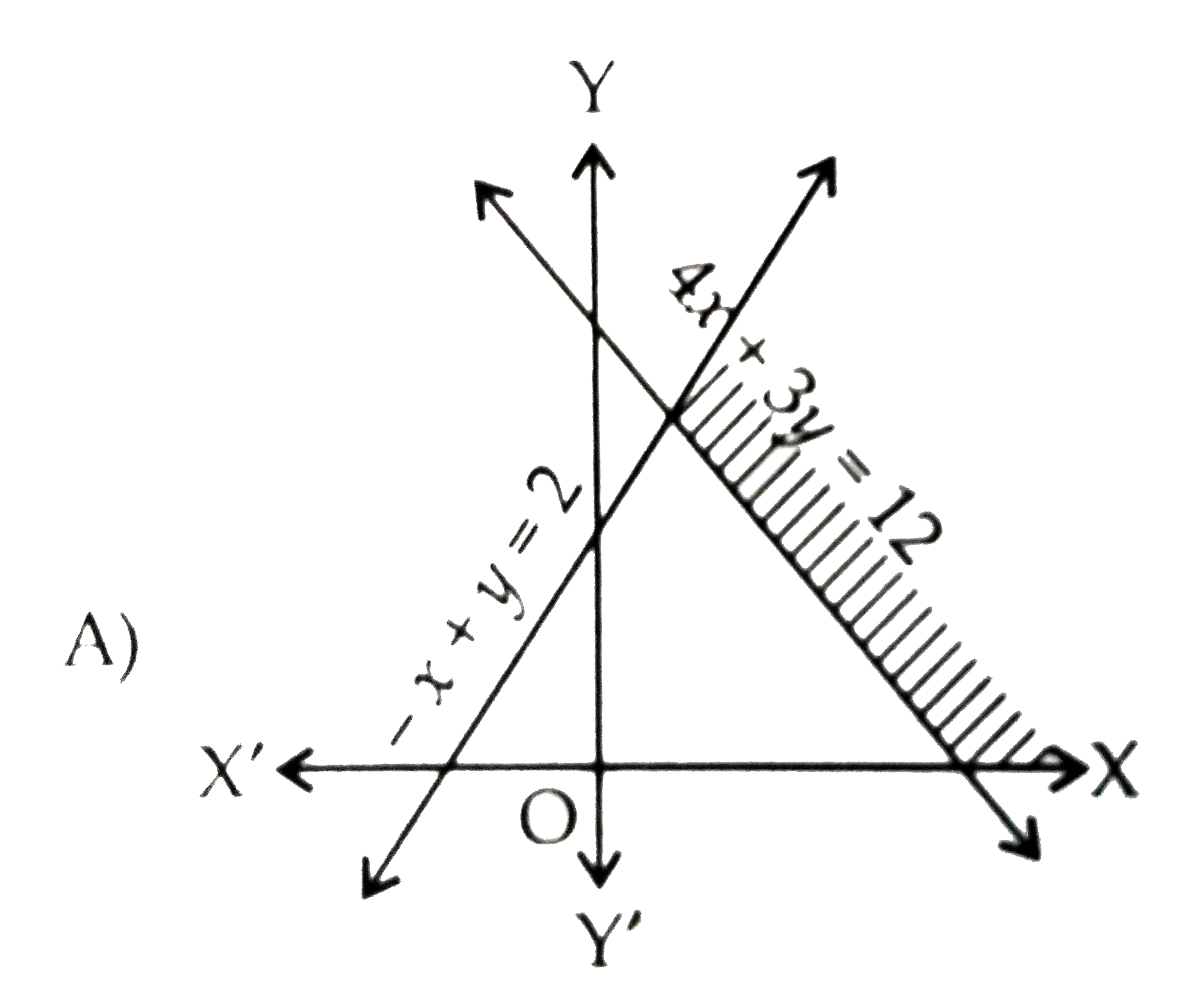 B
B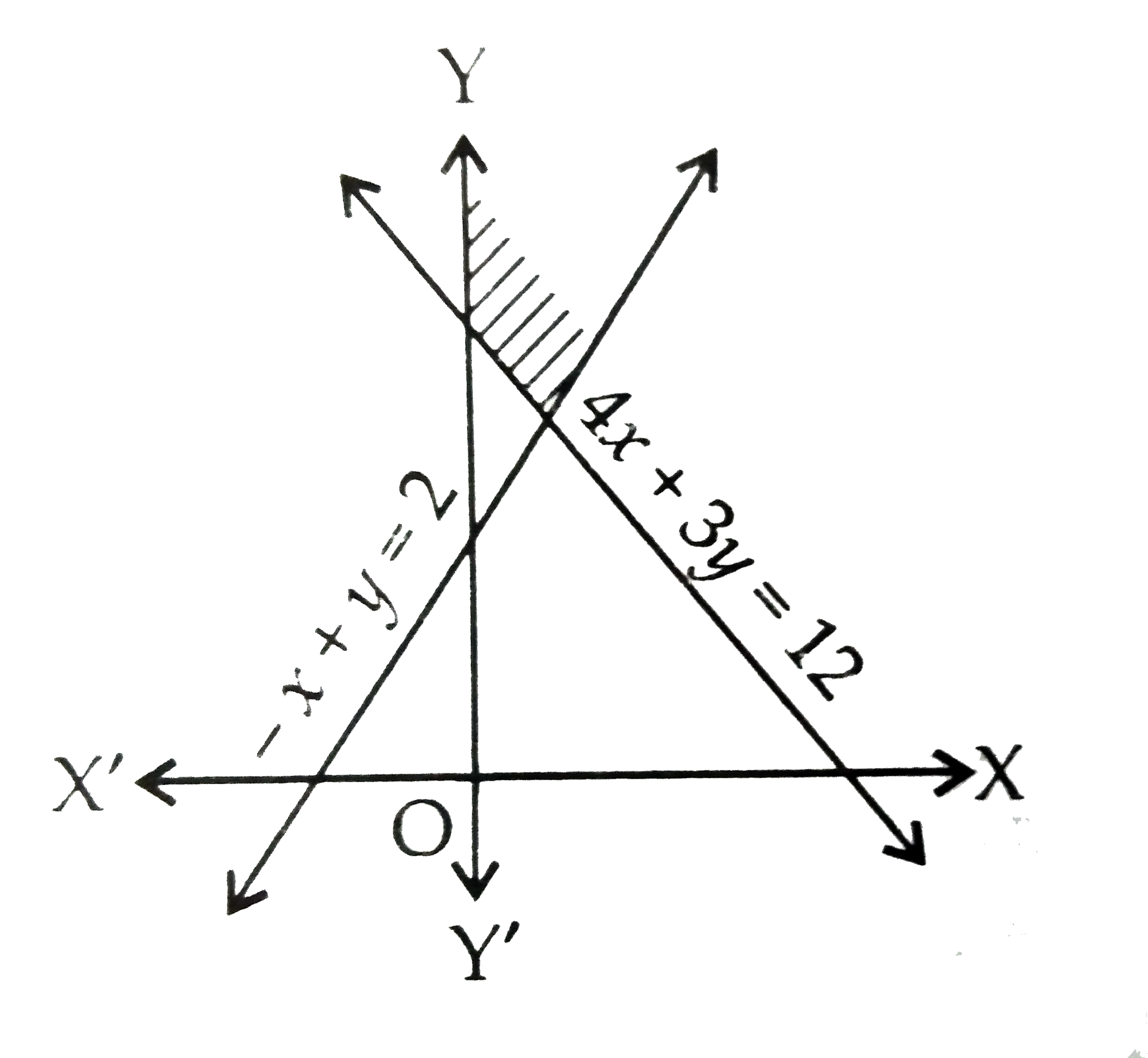 C
C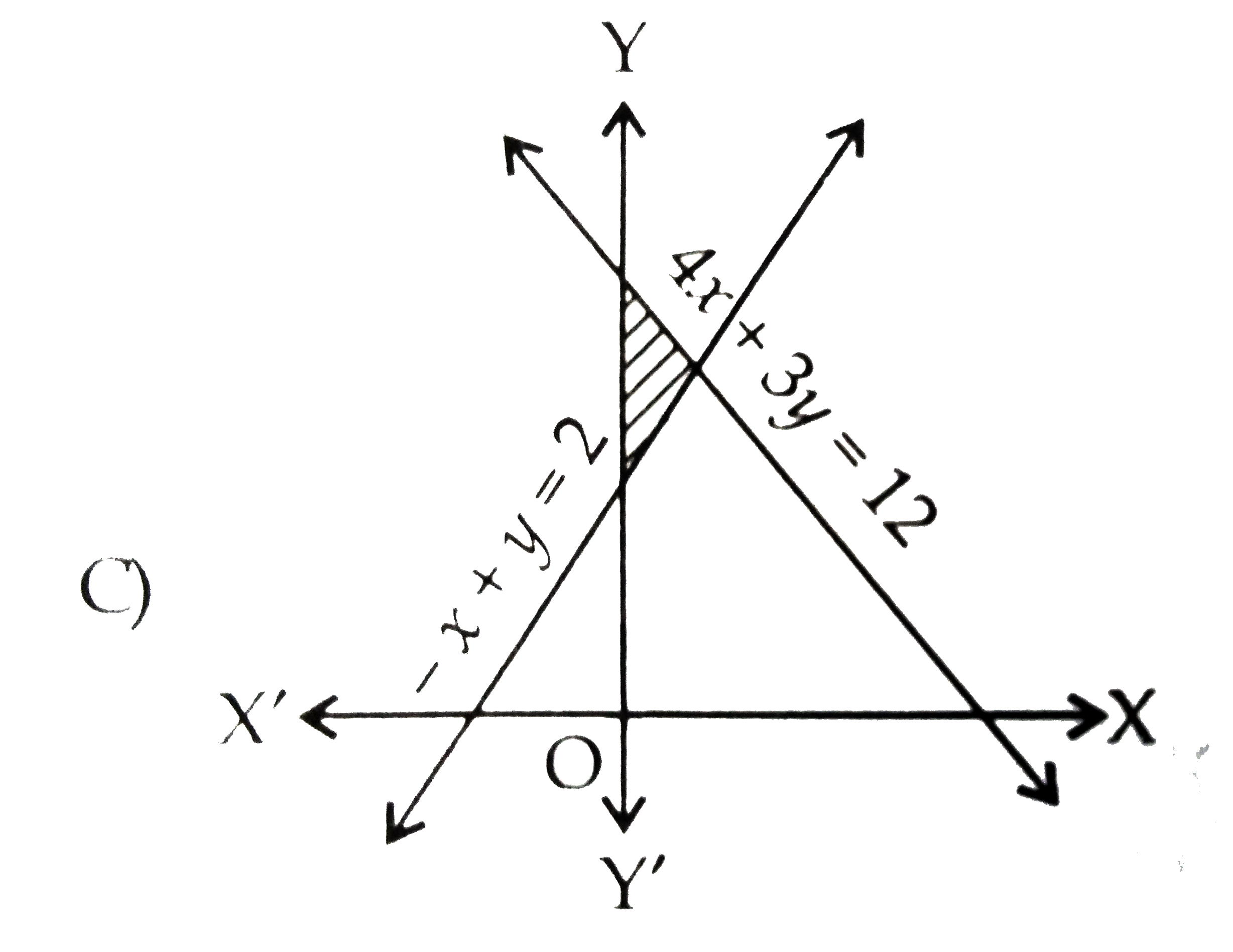 D
D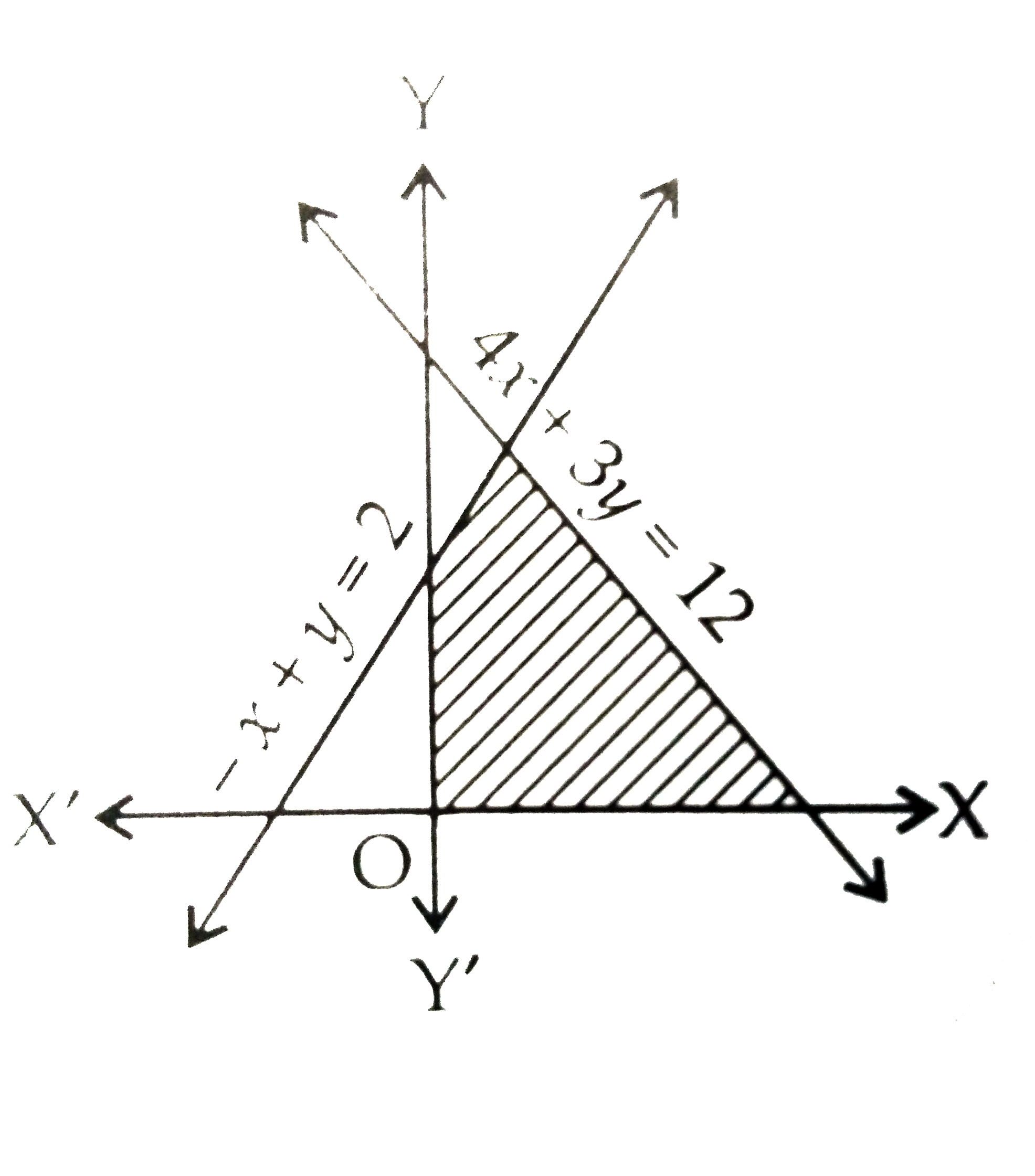
- Question 3 - Select One
The area (in sdq. Units) of the region {(x,y):y2≥2x and x2+y2≤4x,x≥0,y≥0} is
Aπ−83Bπ−4√23Cπ2−2√23Dπ−43
Solve the following inequation graphically x+y≥0,3x+4y≤12,x−2y≤2,x≥0,y≥0.
View SolutionIf 4x+5y≤20,x+y≥3,x≥0,y≥0 maximum 2x + 3y is
View SolutionNumber of integral solutions of 2x+y+z=10(x≥0,y≥0,Z≥0) is
View SolutionShaded, region of the constraints x+y≥5,2x+3y≤18,4x+3y≤24,x≥0,y≥0 is
View SolutionThe minimum value of z=x+2y subject to x+2y≥50,2x−y≤0,2x+y≤100,x≥0,y≥0 is
View Solution

