If (mi,1mi),i=1,2,3,4 are four distinct points on a circle, show that m1m2m3m4=1
0
2
-1
1
Step by step video & image solution for If (m_i , 1/m_i), i= 1, 2, 3, 4 are four distinct points on a circle, show that m_1 m_2 m_3 m_4 = 1 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Particles of masses m1 and m2 are at a fixed distance apart. If the gravitational field strength at m1 and m2 are →I1 and →I2 respectively. Then,
Am1→I1+m2→I2=0Bm1→I2+m2→I1=0Cm1→I1−m2→I2=0Dm1→I2−m2→I1=0Four particle of masses m1=2m,m2=4m,m3=mandm4 are placed at four corners of a square. What should be the value of m4 so that the centres of mass of all the four particle are exactly at the centre of the square ?
 A3 mB5 mC8 mDnone of these
A3 mB5 mC8 mDnone of theseIf m1 and m2 are the slopes of tangents to the circle x2+y2=4 from the point (3,2), then m1−m2 is equal to
A512B125C32D0
ABCD is a square of length a, a∈N, a > 1. Let L1,L2,L3... be points on BC such that BL1=L1L2=L2L3=....1 and M1,M2,M3,....be points on CD such that CM1=M1M2=M2M3=...=1. Then a−1∑n=1((ALn)2+(LnMn)2) is equal to :
View SolutionFind the value of m
m−13−m−24=1
View SolutionLet li,mi,ni;i=1,2,3 be the direction cosines of three mutually perpendicular lines referred to an orthogonal cartesian co–ordinate system, then prove that A=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦is an orthogonal matrix.
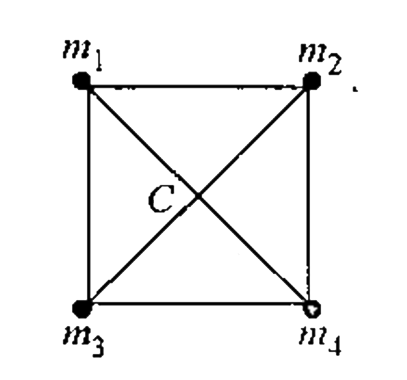
View SolutionFour particle of masses m1=2kg,m2=4kg,m3=1kg and m4 are placed at four corners of a square as shown in figure. Can mass of m4 be adjusted I such a way that the centre of mass of system will be at the centre of the square C.
View SolutionIf m+1m−2=4, find
m2+m+1=?
View Solution
