A particle of mass m and charge q enters a region of magnetic field (as shown) with speed v at t = 0. There is a region in which the magnetic field is absent as shown. The particle after entering the region collide elastically with a rigid wall. Time t after which the velocity of particle become antiparallel to its initial velocity is -

m2qB(π+4)
mqB(π+2)
m4qB(π+2)
m4qB(2π+3)
Step by step video & image solution for A particle of mass m and charge q enters a region of magnetic field (as shown) with speed v at t = 0. There is a region in which the magnetic field is absent as shown. The particle after entering the region collide elastically with a rigid wall. Time t after which the velocity of particle become antiparallel to its initial velocity is - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle of mass m and charge q enters a region of magnetic field (as shown) with speed v. There is a region in which the magnetic field is absent (as shown). The particleafter entering this region collides elastically with a riggid wall. The time after which the velocity of the purticle becomes anti-parallel to its initial velocity is. mαqB(π+β). Find (α+β).
View SolutionA particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
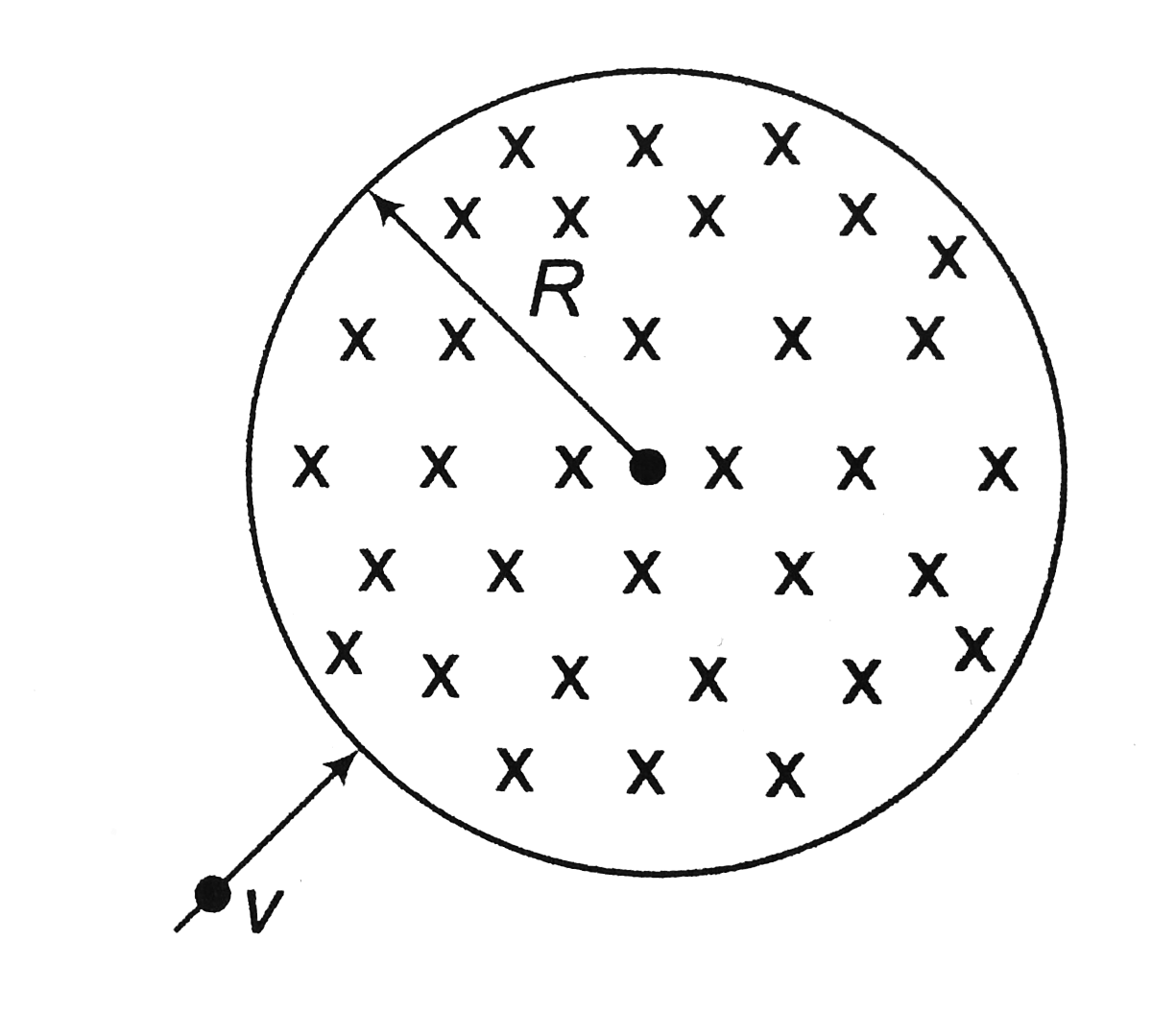
View Solution
Knowledge Check
A particle of mass m and charge q enters a magnetic field B perpendicularly with a velocity v, The radius of the circular path described by it will be
ABq/mvBmq/BvCmB/qvDmv/BqA particle enters the region of a uniform magnetic field as shown in figure. The path of the particle inside the field is shown by dark line. The particle is :
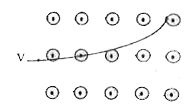 Aelectrically neutralBpositively chargedCnegatively chargedDinformation given is inadequate
Aelectrically neutralBpositively chargedCnegatively chargedDinformation given is inadequateA charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
AmvsinθqBBmvqBsinθCmvqBDmvtanθqB
A particle of mass m and charge +q enters a region of magnetic field with a velocity v, as shown in Fig. 1.93.
a. Find the angle subtended by the circular arc described by it in the magnetic field.
b. How long does the particle stay inside the magnetic field?
c. If the particle enters at E, what is the intercept EF?

View SolutionA particle of mass m and charge q moving with velocity v enters the region of uniform magnetic field at right angle to the direction of its motion. How does its kinetic energy get affected?
View SolutionA charged particle (q,m) enters uniform magnetic field B at angle α shown in figure with speed v0. Find
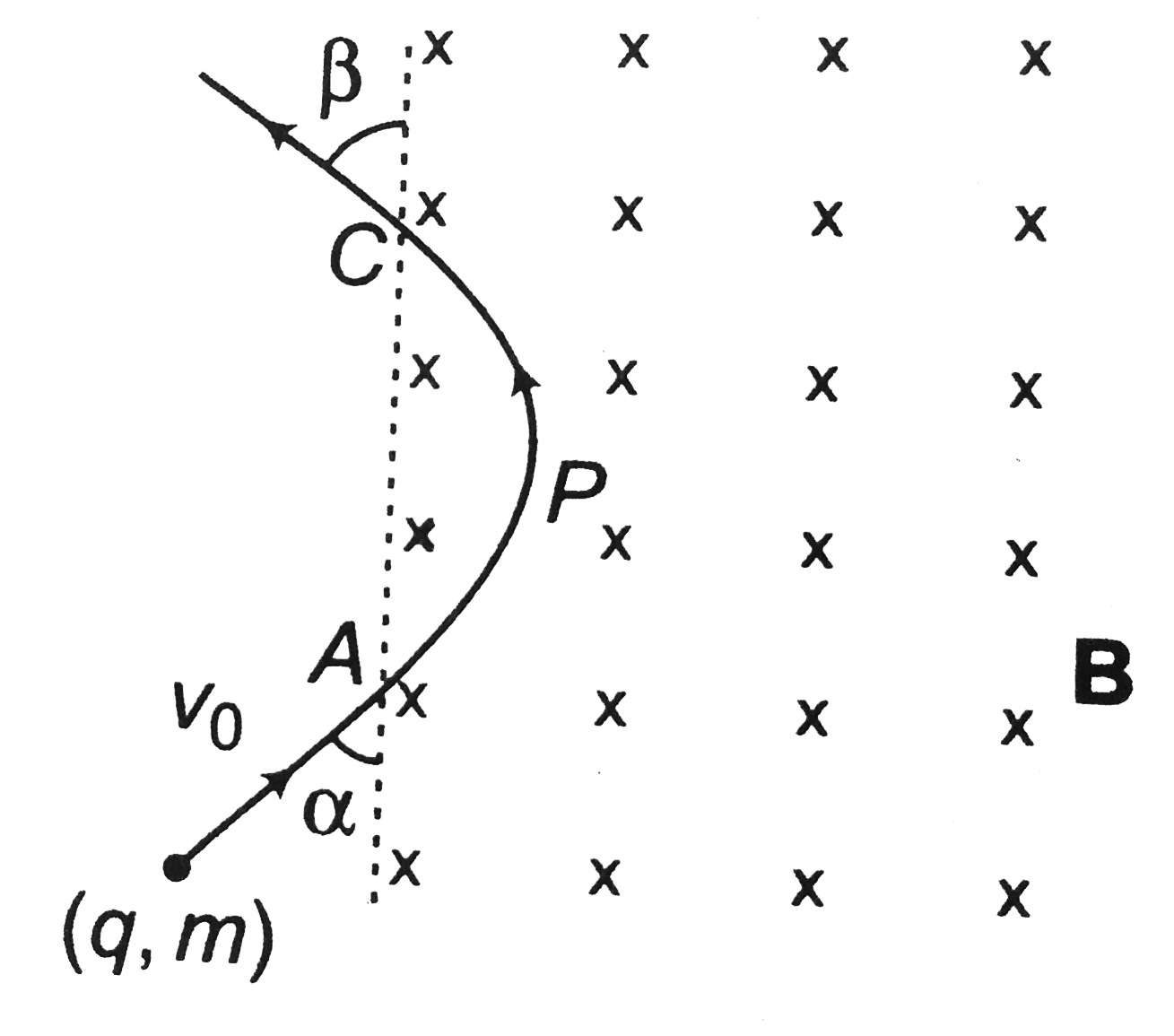
a. The angle β at which it leves the magnetic field
b. time spent by the particle in magnetic field and
c. the distance C.
View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View SolutionA charged particle enters in a uniform magnetic field with a certain velocity. The power delivered to the particle by the magnetic field depends on
View Solution
