ABC is a triangle right angled at 'C'. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. Show that : CM=MA=12AB .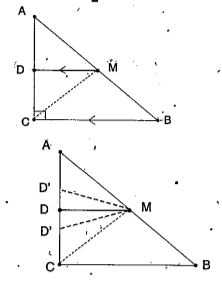
Solution in Telugu
Step by step video & image solution for ABC is a triangle right angled at 'C'. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. Show that : CM = MA = 1/2 AB . by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Make 2 more sentences and check whether they are statements or not? Give reasons.
View SolutionCan we represent all rational numbers pictorially ?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionMatch the following Column A to Column B
View SolutionMatch the following Column A to Column B
View SolutionMatch the following Column A to Column B
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य - बिंदु M से होकर BC के समांतर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि
(i) D भुजा AC का मध्य - बिंदु है। (ii ) MD⊥AC है
(iii) CM=MA=12AB है।
View SolutionABC is a right angle in a right triangle ABC. Prove the following if the line drawn parallel to BC through the midpoint M of hypotenuse AB intersects AC at D. CM=MA = 1/2 AB
View SolutionABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and Parallel to BC intersects AC at D. Show that
(i) D is the midpoint of AC
(ii) MD⊥AC
(iii) CM=MA=12AB.
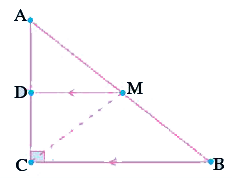
View SolutionABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and Parallel to BC intersects AC at D. Show that
(i) D is the midpoint of AC
(ii) MD⊥AC
(iii) CM=MA=12AB.
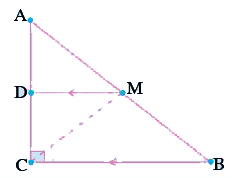
View SolutionABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and Parallel to BC intersects AC at D. Show that
(i) D is the midpoint of AC
(ii) MD⊥AC
(iii) CM=MA=12AB.
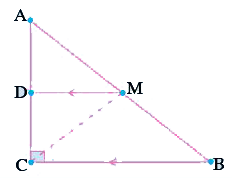
View Solution