A car travels from A to B and returns to its original position.
The distance between A and B is 2000 m.
The car takes 5 min to travel from A to B but takes 8 min to travel back from B to A. Is the speed of the car greater while going from A to B or while travelling back from B to A?
To determine whether the speed of the car is greater while going from A to B or while traveling back from B to A, we can follow these steps:
Step 1: Identify the distances and times
- The distance from A to B (D) = 2000 m
- Time taken to travel from A to B (t1) = 5 minutes
- Time taken to travel back from B to A (t2) = 8 minutes
Step 2: Convert time from minutes to seconds
Since speed is typically expressed in meters per second (m/s), we need to convert the time from minutes to seconds.
- 1 minute = 60 seconds
- t1 = 5 minutes = 5 × 60 = 300 seconds
- t2 = 8 minutes = 8 × 60 = 480 seconds
Step 3: Calculate the speed from A to B (S1)
Using the formula for speed:
Speed=DistanceTime
For the journey from A to B:
S1=Dt1=2000m300s
S1=2000300≈6.67m/s
Step 4: Calculate the speed from B to A (S2)
Using the same formula for speed:
For the journey from B to A:
S2=Dt2=2000m480s
S2=2000480≈4.17m/s
Step 5: Compare the speeds
Now we can compare the two speeds:
- Speed from A to B (S1) ≈ 6.67 m/s
- Speed from B to A (S2) ≈ 4.17 m/s
Since 6.67 m/s > 4.17 m/s, the speed of the car is greater while going from A to B.
Conclusion
The speed of the car is greater while going from A to B than while traveling back from B to A.
---
- The distance from A to B (D) = 2000 m
- Time taken to travel from A to B (t1) = 5 minutes
- Time taken to travel back from B to A (t2) = 8 minutes
Since speed is typically expressed in meters per second (m/s), we need to convert the time from minutes to seconds.
- 1 minute = 60 seconds
- t1 = 5 minutes = 5 × 60 = 300 seconds
- t2 = 8 minutes = 8 × 60 = 480 seconds
Using the formula for speed:
Speed=DistanceTime
For the journey from A to B:
S1=Dt1=2000m300s
S1=2000300≈6.67m/s
Using the same formula for speed:
For the journey from B to A:
S2=Dt2=2000m480s
S2=2000480≈4.17m/s
Now we can compare the two speeds:
- Speed from A to B (S1) ≈ 6.67 m/s
- Speed from B to A (S2) ≈ 4.17 m/s
The speed of the car is greater while going from A to B than while traveling back from B to A.
Topper's Solved these Questions
- ICSE ANNUAL EXAMINATION -2020BOOK - ICSECHAPTER - ICSE ANNUAL EXAMINATION -2020EXERCISE - SECTION-II
45 Videos
- HEAT AND ENERGYBOOK - ICSECHAPTER - HEAT AND ENERGYEXERCISE - EXERCISE -6(D) Multiple Choice Question)
4 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - 3(E) (Numericals)
31 Videos
Similar Questions
A car travels from A to B and returns to its original position.
The distance between A and B is 2000 m.
Find the total displacement of the car.
View SolutionA car travels from A to B and returns to its original position.
The distance between A and B is 2000 m.
When can the magnitude of distance and displacement be equal for a body in motion?
View Solution
Knowledge Check
The distance between cities A and B car travels from A to B at 60 miles per hour and returns from B to A long the same route at 40 miles per hour. What is the averge speed for the round trip?
A48B50C56D58
A particle travels from A to B path shown in figure, then the displacement of particle is :
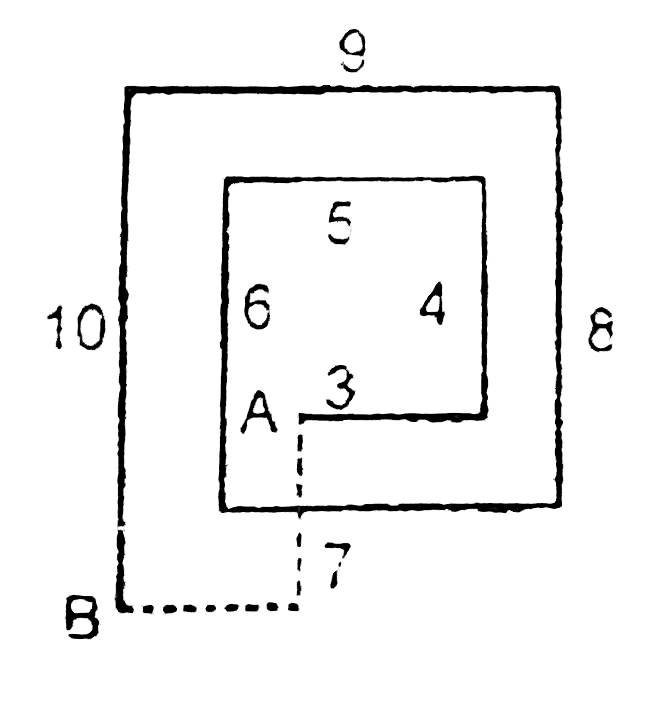 .
.
View SolutionA car moves from O to D along the path OABCD shown in fig.
What is distance travelled and net displacement.
View SolutionTwo cars started simultaneously towards each other from towns A and B which are 480 km apart.It took first car travelling from A to B 8 hours to cover the distance and second car travelling form B to A in 12 hours.Determine when do the car meet after starting and at what distance from town A.Assuming that both the cars travelled with constant speed.
View SolutionA person wants to go from station A to station C via station b. There are three routes from A to B four routes from B to C. In how many ways can he travel from A to C?
View SolutionA car travels a distance of 75 km in 1.5 hours
What is its speed ?
View SolutionA car travels for 20 min with a constant speed of 54 km h−1 Find the distance travelled by the car.
View SolutionA car travelled from city A to city B with a uniform speed of 52 27 km per hour. Find the 3 ' distance between the two cities, if it took 438 hours for the car to reach city B from city A.
View Solution
