Non Inertial Frame
Step by step video solution for Non Inertial Frame by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023समान प्रश्न
The no.of correct statements are 1) The apparent weight of a freely falling body is zero II) Applied force is a example of pseudo force III) Pseudo forces exist for observers only in non inertial frames, such forces have no existence relative to an inertial frame
View SolutionDefine inertial frame of reference.
View Solution
ज्ञान जांच
Assertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.AIf both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.BIf both Assertion & Reason are True but Reason is not correct explanation of the Assertion.CIf Assertion is Trie but the Reason is False.DIf both Assertion & Reason are falseAssertion:− A particle on earth found to be at rest when seen from a frame U1 and moving with a constant velocity when seen from another frame U2. Then both frames may be non−inertial.
Reason :− A reference frame attached to the earth must be an inertial frame.AIf both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.BIf both Assertion & Reason are True but Reason is not a correct explanation of the Assertiion.CIf Assertion is True but the Reason is False.DIf both Assertion & Reason are FalseAn inertial frame of reference is, by definition,
Aa frame moving with uniform velocity w.r.t. earthBa frame moving with velocity w.r.t our SunCa frame which is not rotatingDa frame in which Newton's first law of motion is valid.
An inertial frame of reference is, by definition,
View SolutionThese questions consists of two statements each printed as Assertion and Reason. While answering these question you are required to choose any one of the following four responses
Assertion Earth is an inertial frame.
Reason A frame in motion is sometimes an inertial frame and sometimes a non-inertial.
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
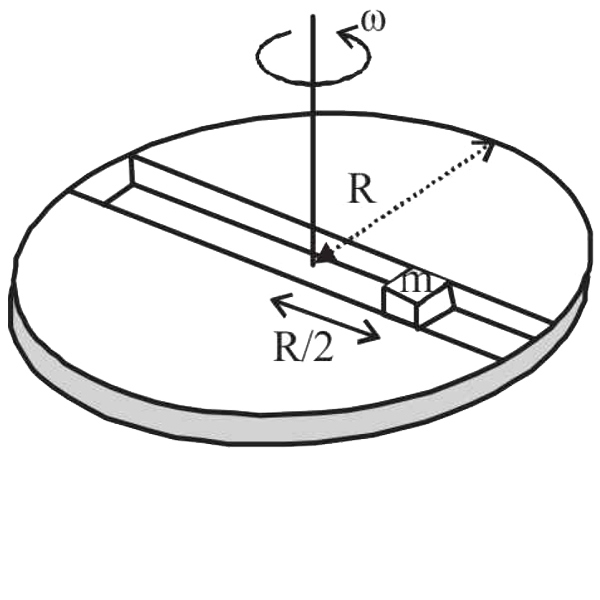
The distance r of the block at time is
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
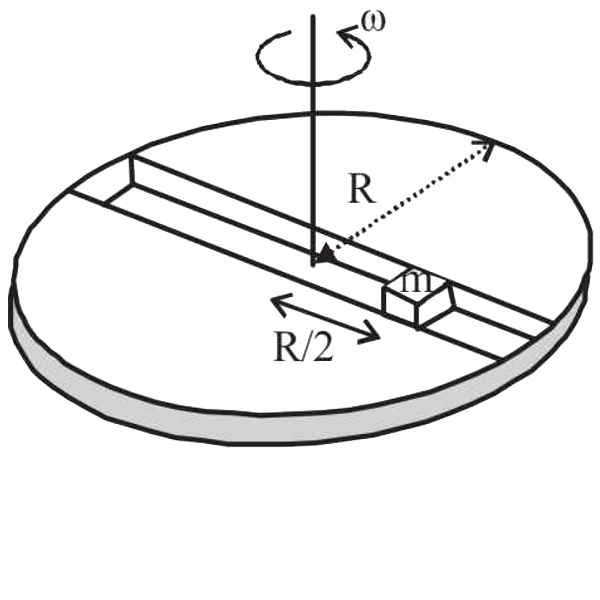
The net reaction of the disc on the block is
View SolutionAssuming earth to be an intertial frame, an example for inertial frame observer is:
View Solution
