For any three events A. B.' C show thatP(A∪B∪C)=P(A)+P(B)+P(C)−P(A∩B)−P(B∩C)−P(C∩A)+P(A∩B∩C)Solution in Bengali
Step by step video & image solution for For any three events A. B.' C show thatP(AcupBcupC)=P(A)+P(B)+P(C)-P(AcapB)-P(BcapC)-P(CcapA)+P(AcapBcapC) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Which is nul set
View SolutionIf n (x) = 12, n (Y) = 10 and n (X∩Y)=8, then the value of of n(X∪Y)is
View SolutionFor any three events A, B and C, prove that.
P(A∪B∪C)=P(A)+P(B)+P(C)−P(A∩B)
−P(B∩C)−P(C∩A)+P(A∩B∩C).
View SolutionIf P(A)=12, P(B)=13, P(C)=12 and P(A∩B)=P(B∩C)=P(C∩A)=14 and P(A∩B∩C)=18, then the probability that at least one of them appears is
View SolutionFor any two events A and B, shows that
P(AC∩BC)=1 +P(A∩B)−P(A)−P(B).
View SolutionThe probabilities of three events A,B,C are such that P(A)=0.3, P(B)=0.04, P( C) = 0.8 P(A∩B)=0.08
P(A∩C)=0.28,P(A∩B∩C)=0.09 and
P(A∪B∪C)≥0.75. Show that P(B∩C) lies in the interval [0.23,0.48]
View SolutionIf A,B are two events, then show that
P(AB)P(B)+P(ABC)P(BC)=P(A).
View SolutionIf A,B,C are three events in a random experiment, Prove the following.
P(A−B)=P(A)−P(A∩B)
View SolutionFor any two events A,B shows that
P(A∩B)−P(A)P(B)=P(AC)P(B)−P(AC∩B)
=P(A)P(BC)−P(A∩BC)
View SolutionIf A,B, are two events with P(A∪B)=0.65,andP(A∩B)=0.15, then find the value of P(AC)+P(BC).
View SolutionIf A, B, C are three independent events such that P(A∩B)=12,P(B∩C)=13andP(C∩A)=16, find P(A),P(B)andP(C).
View SolutionIf P(A) = 0.4, P(B)=0.5, P(C) =0.6, P(A∩B) = 0.2, P(B∩C) = 0.3, P(C∩A) = 0.25, P(A∩B∩C)=0.1 then P(A∪B∪C)=
View SolutionA, B and C are events associated with a random experiment such that
P(A) = 0.3,
P(B) = 0.4, P(C) = 0.8, P(A∩B) = 0.08, P(A∩C) =0.28 and P(A∩B∩C) = 0.09. If
P(A∪B∪C)≥0.75 Then prove that P(B∩C) lies in the interval [0.23,0.48].
View SolutionIf A, B C are three events associated with a random experiment, prove that P(A∪B∪C)=P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−
P(B∩C)+P(A∩B∩C).
View SolutionThe accompanying Venn diagram shows three events, A,B, and C, also the probabilities of the various intersections (for instance, P(A∩B)=.07 ). Determine
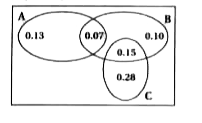
(i) P(A)
(ii) P(B∩C')
(iii) P(A∪B)
(iv) P(A∩B')
(v) P(B∩C)
(vi) Probability of exactly one of the three occurs.
View Solution
