In positively skewed distribution. Solution in Bengali
a) mean <median< mode
b) mean = median = mode
c) mean>median>mode
d) none of these
Step by step video & image solution for In positively skewed distribution. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Write down all the subsets of the following sets
ϕ
View SolutionIf A={2,4,6,8}then
View SolutionShow that positive odd integral powers of a skew-symmetric matrix are skew-symmetric and positive even integral powers of a skew-symmetric matrix are symmetric.
View SolutionIf for a moderately skewed distribution, mode = 60 and mean = 66, then median =
View Solution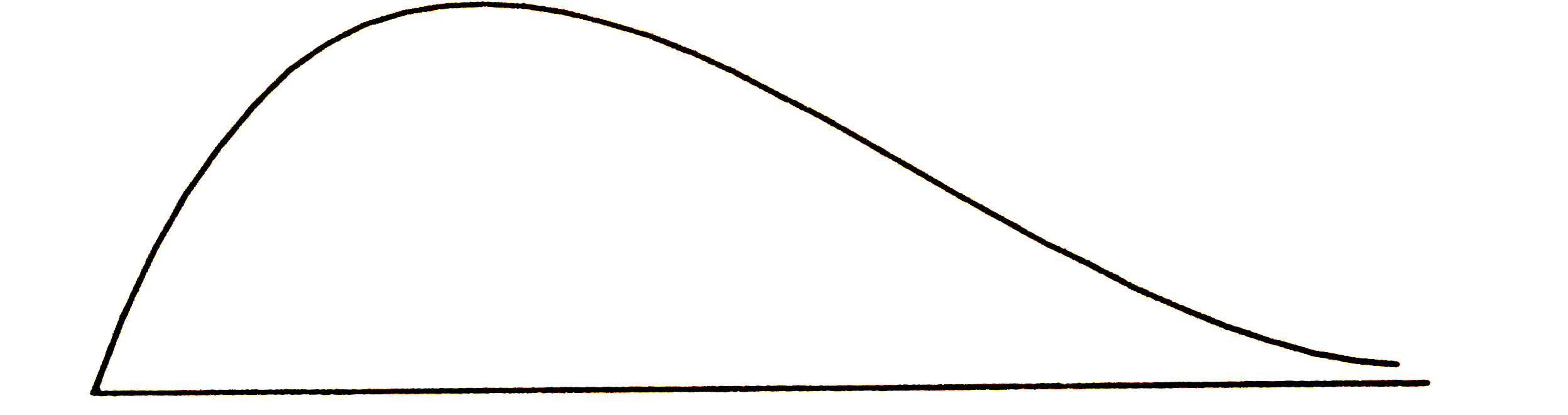
The frequency curve for the distribution of income in a region is positively skewed as shown in the figure above. Then, for this distribution
View SolutionFor a moderately skewed distribution
View SolutionIn a moderately skewed distribution, the values of mean and median are 5 and 6 respectively. The value of mode for such distribution is
View SolutionShow that positive odd integral powers of a skew-symmetric matrix are skew-symmetric and positive even integral powers of a skew-symmetric matrix are symmetric.
View SolutionShow that positive odd integral powers of a skew-symmetric matrix are skew-symmetric and positive even integral powers of a skew-symmetric matrix are symmetric.
View SolutionShow that positive odd integral powers of a skew-symmetric matrix are skew-symmetric and positive even integral powers of a skew-symmetric matrix are symmetric.
View SolutionWrite any three measures of skewness of a distribution.
View SolutionWrite the empirical relation between mean, median and made for a moderately skew distribution.
View SolutionDistinguish between positive skewness and negative skewness.
View SolutionFor a positively skewed distribution, what is the relation between mean, median and mode?
View SolutionIn a moderately skew distribution A.M. = 24.6 and the median = 26.1. Find the value of the mode.
View Solution
