A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
decreases as r increases for r<R and r>R
increases as r increases for r<R and r>R
zero as r increases for r<R, decreases as r increases for r>R
zero as r increases for r<R, increases for r>R
The correct Answer is:C
To determine the electric field due to a hollow metal sphere of radius R at a distance r from its center, we will analyze two cases: when r<R (inside the sphere) and when r>R (outside the sphere).
1. Understanding the Setup:
- We have a hollow metal sphere with radius R that is uniformly charged with total charge Q.
- We need to find the electric field E at a distance r from the center of the sphere.
2. Case 1: Inside the Sphere (r<R):
- According to Gauss's law, the electric field inside a conductor in electrostatic equilibrium is zero.
- Since there is no charge enclosed within a Gaussian surface that lies inside the hollow region of the sphere, we can write:
E⋅A=Qenclosedϵ0
- Here, A is the area of the Gaussian surface and Qenclosed=0.
- Therefore, we have:
E⋅0=0⟹E=0
- Thus, for r<R, the electric field E=0.
3. Case 2: Outside the Sphere (r>R):
- For a point outside the hollow sphere, we can consider the entire charge Q to be concentrated at the center of the sphere.
- Applying Gauss's law again, we take a Gaussian surface of radius r (where r>R):
E⋅A=Qenclosedϵ0
- The area A of the Gaussian surface is 4πr2 and Qenclosed=Q.
- Thus, we have:
E⋅4πr2=Qϵ0
- Solving for E:
E=Q4πϵ0r2
- This shows that the electric field E outside the sphere decreases with the square of the distance r from the center.
4. Conclusion:
- For r<R, E=0.
- For r>R, E decreases as r increases.
- Therefore, the correct option is: "0 as r increases for r<R and decreases as r increases for r>R."
- We have a hollow metal sphere with radius R that is uniformly charged with total charge Q.
- We need to find the electric field E at a distance r from the center of the sphere.
- According to Gauss's law, the electric field inside a conductor in electrostatic equilibrium is zero.
- Since there is no charge enclosed within a Gaussian surface that lies inside the hollow region of the sphere, we can write:
E⋅A=Qenclosedϵ0
- Here, A is the area of the Gaussian surface and Qenclosed=0.
- Therefore, we have:
E⋅0=0⟹E=0
- Thus, for r<R, the electric field E=0.
- For a point outside the hollow sphere, we can consider the entire charge Q to be concentrated at the center of the sphere.
- Applying Gauss's law again, we take a Gaussian surface of radius r (where r>R):
E⋅A=Qenclosedϵ0
- The area A of the Gaussian surface is 4πr2 and Qenclosed=Q.
- Thus, we have:
E⋅4πr2=Qϵ0
- Solving for E:
E=Q4πϵ0r2
- This shows that the electric field E outside the sphere decreases with the square of the distance r from the center.
- For r<R, E=0.
- For r>R, E decreases as r increases.
- Therefore, the correct option is: "0 as r increases for r<R and decreases as r increases for r>R."
Similar Questions
A non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionA solid sphere of radius R has a charge +2Q. A hollow spherical concentric with the first sphere that has net charge -Q.
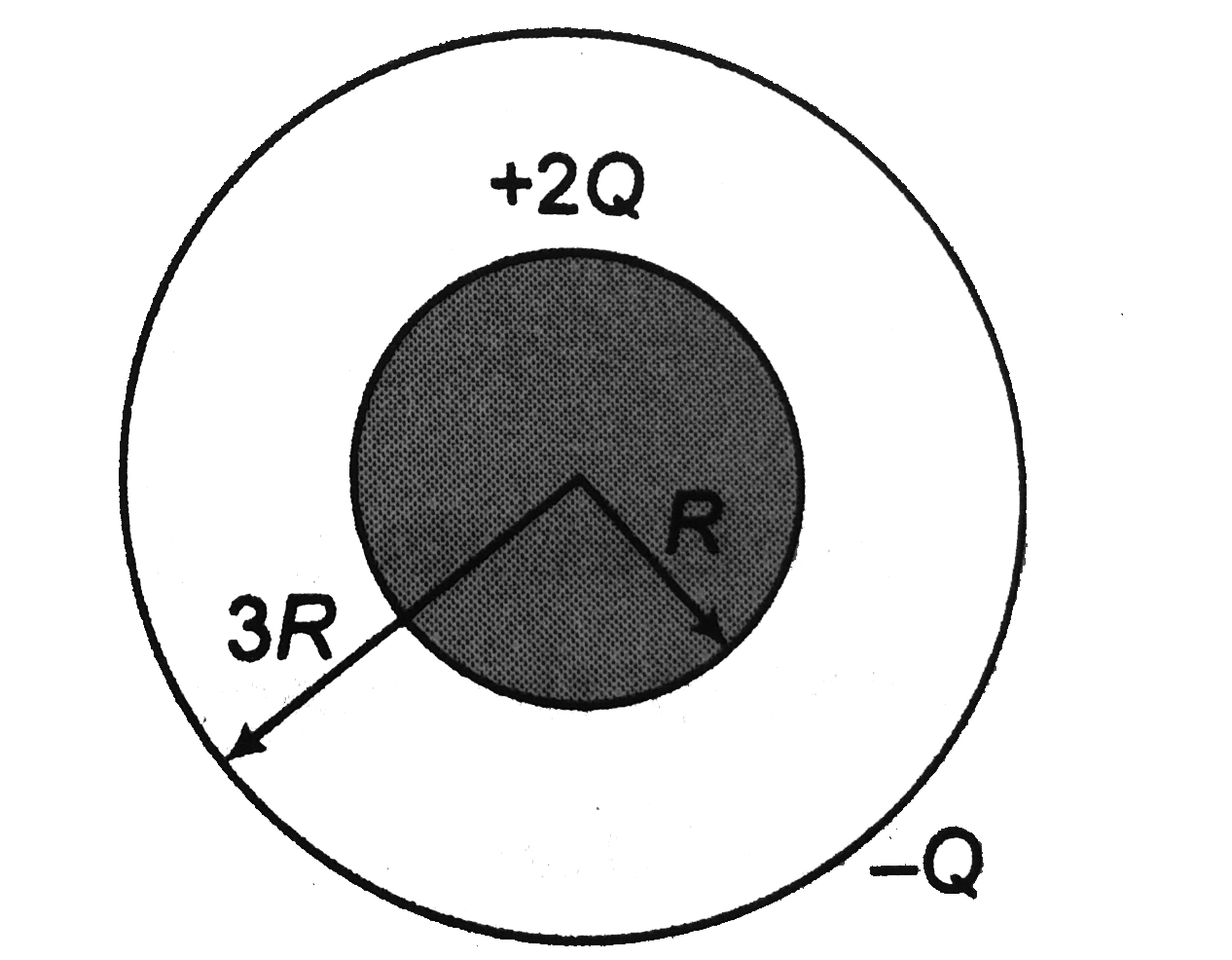
(a) Find the electric field between the spheres at a distance r from the centre of the inner sphere. [R<r<3R]
(b) Calculate the potential difference between the spheres.
(c) What would be the final distribution of charges, if a conducting wire joins the spheres?
(d) Instead of (c), if the inner sphere is earthed, what is the charge on it?View Solution
Knowledge Check
- Question 1 - Select One
Let ρ(r)=QrπR4 be the charge density distribution for a soild sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
AQr214πε0R4BQr213πε0R4C0DQ4iε0r21
Figure shows a uniformly charged sphere of radius R and total charge Q. A point charge q is situated outside the sphere at a distance r from centre of sphere. Find out the following :
(i) Force acting on the point charge q due to the sphere.
(ii) Force acting on the sphere due to the point charge.
 View Solution
View SolutionA solid sphere of radius R is charged uniformly. The electrostatic potential V is plotted as a function of distance r from the centre of th sphere. Which of the following best represents the resulting curve?
View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be (r>R).
 View Solution
View SolutionThe electric field intensity at a distance 20cm from the centre of a uniformly charged non conducting solid sphere of radius 10cm is E.Then what is the electric field intensity at a distance 5cm from the centre it will be.....
View SolutionLet P(r)=QπR4r be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'p' inside the sphere at distance r1 from the centre of the sphere, the magnitude of electric field is:
View SolutionConsider an atom with atomic number Z as consisting of a positive point charge at the centre and surrounded by a distribution of negative electricity uniformly distributed within a sphere of radius R. The electric field at a point inside the atom at a distance r from the centre is
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View Solution

