A solid cylinder of mass 2 kg and radius 4 cm rotating about its axis at the rate of 3 rpm. The torque required to stop after 2π revolutions is :
2×106Nm
2×10−6Nm
2×10−3Nm
12×10−4Nm
The correct Answer is:B
To solve the problem step by step, we will follow these calculations:
Step 1: Convert the initial angular velocity from rpm to rad/s
Given:
- Initial speed = 3 rpm
To convert this to radians per second:
ω0=3 rpm×2π rad1 rev×1 min60 s=3×2π60=6π60=π10 rad/s
Step 2: Determine the angular displacement in radians
We need to stop the cylinder after 2π revolutions. The angular displacement (θ) in radians is:
θ=2π rev×2π rad/rev=4π2 rad
Step 3: Use the equation of motion for angular motion
We will use the equation:
ω2=ω20+2αθ
Where:
- ω (final angular velocity) = 0 (since we want to stop the cylinder)
- ω0=π10 rad/s
- θ=4π2 rad
Substituting the values:
0=(π10)2+2α(4π2)
0=π2100+8π2α
Rearranging gives:
8π2α=−π2100
α=−1800 rad/s2
Step 4: Calculate the moment of inertia (I) of the solid cylinder
The moment of inertia of a solid cylinder rotating about its axis is given by:
I=12mr2
Where:
- m=2 kg
- r=4 cm=0.04 m
Calculating I:
I=12×2×(0.04)2=12×2×0.0016=0.0016 kg m2
Step 5: Calculate the torque (τ)
Using the formula for torque:
τ=Iα
Substituting the values:
τ=0.0016×(−1800)=−0.0016800=−2×10−6 N m
The negative sign indicates that the torque is applied in the opposite direction of the rotation.
Final Answer
The torque required to stop the cylinder after 2π revolutions is:
τ=2×10−6 N m
---
Given:
- Initial speed = 3 rpm
ω0=3 rpm×2π rad1 rev×1 min60 s=3×2π60=6π60=π10 rad/s
We need to stop the cylinder after 2π revolutions. The angular displacement (θ) in radians is:
θ=2π rev×2π rad/rev=4π2 rad
We will use the equation:
ω2=ω20+2αθ
Where:
- ω (final angular velocity) = 0 (since we want to stop the cylinder)
- ω0=π10 rad/s
- θ=4π2 rad
0=(π10)2+2α(4π2)
0=π2100+8π2α
Rearranging gives:
8π2α=−π2100
α=−1800 rad/s2
The moment of inertia of a solid cylinder rotating about its axis is given by:
I=12mr2
Where:
- m=2 kg
- r=4 cm=0.04 m
I=12×2×(0.04)2=12×2×0.0016=0.0016 kg m2
Using the formula for torque:
τ=Iα
Substituting the values:
τ=0.0016×(−1800)=−0.0016800=−2×10−6 N m
The torque required to stop the cylinder after 2π revolutions is:
τ=2×10−6 N m
Similar Questions
Knowledge Check
- Question 1 - Select One
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2 - Question 2 - Select One
An solid cylinder of mass 20kg and radius 20cm rotates about its axis with a angular speed 100rads−1. The angular momentum of the cylinder about its axis is: a) 40 J s b) 400 J s c) 20 J s d) 200 J s
A40 J sB400 J sC20 J sD200 J s - Question 3 - Select One
A hollow cylinder of mass M and radius R is rotating about its axis of symmetry and a solid sphere of same mass and radius is rotating about an axis passing through its centre. It torques of equal magnitude are applied to them, then the ratio of angular accelerations produced is a) 2/5 b) 5/2 c) 5/4 d) 4/5
A43587B43501C43560D43589
A ring of diameter 0.4 m and of mass 10 kg is rotating about its axis at the rate of 1200 rpm. The angular momentum of the ring is
View SolutionA flywheel of mass 100 kg and radius 1 m is rotating at the rate of 420 rev/min. Find the constant retarding torque to stop the wheel in 14 revolutions, the mass is concentrated at the rim. M.I. of the flywheel about its axis of rotation I=mr2.
View SolutionOn the surface of a solid cylinder of mass 2 kg and radius 25 cm a string is wound several times and the end of the string is held stationary while the cylinder is released from rest. What is the acceleration of the cylinder and the tension in the string ?
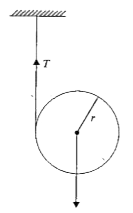 View Solution
View SolutionA solid cylinder of mass 2 kg and radius 0.2m is rotating about its own axis without friction with angular velocity 3 rads/s. A particle of mass 0.5 kg and moving with a velocity 5 m/s strikes the cylinder and sticks to it as shown in figure. The angular momentum of the cylinder before collision will be?
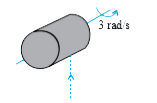 View Solution
View SolutionA soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s−1 . Angular momentum of the cylinder is
View Solution

