Two particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed uA and uB respectively. Their time period of rotation is the same. The ratio of angular speed of a to that of B will be:
1:1
rA:rB
υA:υB
rB:rA
The correct Answer is:A
To solve the problem, we need to find the ratio of the angular speeds of two particles A and B that are moving in uniform circular motion.
1. Understanding Angular Speed:
The angular speed (ω) of an object in circular motion is given by the formula:
ω=2πT
where T is the time period of rotation.
2. Given Information:
- Both particles A and B have the same time period of rotation, which means:
TA=TB
- The angular speeds for particles A and B can be expressed as:
ωA=2πTA
ωB=2πTB
3. Finding the Ratio of Angular Speeds:
We need to find the ratio of the angular speed of A to that of B:
ωAωB=2πTA2πTB
Here, the 2π terms cancel out:
ωAωB=TBTA
4. Substituting the Time Periods:
Since TA=TB, we can substitute:
ωAωB=TBTA=TATA=1
5. Conclusion:
Therefore, the ratio of the angular speed of A to that of B is:
ωAωB=1
Final Answer:
The ratio of angular speed of A to that of B is 1:1.
The angular speed (ω) of an object in circular motion is given by the formula:
ω=2πT
where T is the time period of rotation.
- Both particles A and B have the same time period of rotation, which means:
TA=TB
- The angular speeds for particles A and B can be expressed as:
ωA=2πTA
ωB=2πTB
We need to find the ratio of the angular speed of A to that of B:
ωAωB=2πTA2πTB
Here, the 2π terms cancel out:
ωAωB=TBTA
Since TA=TB, we can substitute:
ωAωB=TBTA=TATA=1
Therefore, the ratio of the angular speed of A to that of B is:
ωAωB=1
The ratio of angular speed of A to that of B is 1:1.
Similar Questions
Two buses A and B are moving around concentric circular pathe of radii rA and rB If the two buses complete the circular paths in the sme time. The ratio on their linear speeds is
View SolutionTwo buses A and B are moving around concentric circular pathe of radii rA and rB If the two buses complete the circular paths in the sme time. The ratio on their linear speeds is
View SolutionA particle is moving in a circle with uniform speed its motion is
View SolutionTwo cars of masses m1 andm2 are moving in circles od radii r1andr2. Their speeds are such that they complete one revolution in the same time. The ratio of their angular speed is :
View SolutionTwo cars A and B are going around concentric circular paths of τA and τB. If the two cars complete the circular paths in the same time then the ratio of angular speeds of A and B is
View SolutionTwo particle move in concentric circles of radii r1 and r2 such that they maintain a straight line through the center. The ratio of their angular velocities is:
View SolutionA system of binary stars of mass mA and mB are moving in circular orbits of radii rA and rB respectively. If TA and TB are at the time periods of masses mA and mB respectively then
View SolutionTwo racing cars of masses m1 and m2 are moving in circles of radii r1 and r2 respectively. Their speeds are such that each makes a complete circle in the same time t. The ratio of the angular speed of the first to the second car is
View SolutionTwo particles A and B are moving as shown in figure. At this moment of time, the angular speed of A with respect to B is?
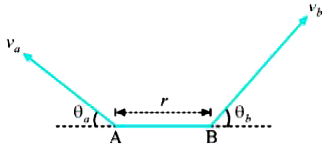 View Solution
View SolutionTwo particles A,B are moving on two concentric circles of radii R1 and R2 with equal angular speed ω. Att=0,their positions and direction of motion are shown in the figure. The relative velocity →Va−→Vb at t=π/2ω is given by :
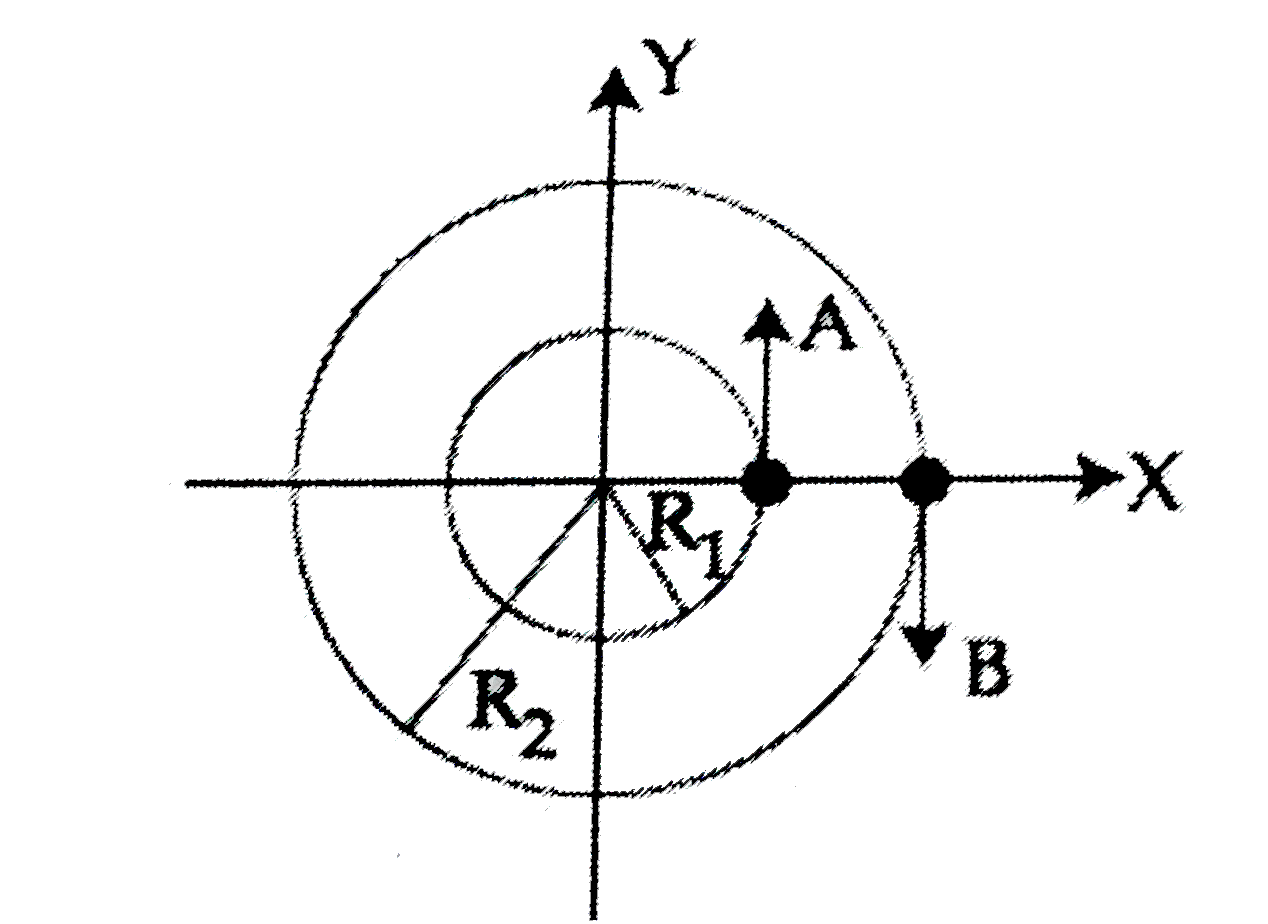 View Solution
View Solution

