A disc of radius 2 m and mass 100kg rolls on a horizontal floor, its centre of mass has speed of . How much work is needed to stop it ?
1J
3J
30 KJ
2J
The correct Answer is:B
To find the work needed to stop a rolling disc, we can use the work-energy theorem, which states that the work done on an object is equal to the change in its kinetic energy.
1. Identify the given values:
- Radius of the disc (r) = 2 m
- Mass of the disc (m) = 100 kg
- Speed of the center of mass (v) = 20 cm/s = 20 × 10^(-2) m/s = 0.2 m/s
2. Calculate the moment of inertia (I) of the disc:
The moment of inertia for a solid disc is given by:
I=12mr2
Substituting the values:
I=12×100kg×(2m)2=12×100×4=200kg m2
3. Calculate the angular velocity (ω):
The angular velocity can be calculated using the relation:
ω=vr
Substituting the values:
ω=0.2m/s2m=0.1rad/s
4. Calculate the initial kinetic energy (KE_initial):
The total kinetic energy of the rolling disc is the sum of translational and rotational kinetic energy:
KEinitial=12Iω2+12mv2
Substituting the values:
KEinitial=12×200kg m2×(0.1rad/s)2+12×100kg×(0.2m/s)2
KEinitial=12×200×0.01+12×100×0.04
KEinitial=1+2=3J
5. Calculate the work done (W):
Since the final kinetic energy (KE_final) when the disc is stopped is 0, the work done to stop the disc is equal to the initial kinetic energy:
W=KEfinal−KEinitial=0−3J=−3J
The work done to stop the disc is 3 J (the negative sign indicates that work is done against the motion).
Final Answer:
The work needed to stop the disc is 3 joules.
- Radius of the disc (r) = 2 m
- Mass of the disc (m) = 100 kg
- Speed of the center of mass (v) = 20 cm/s = 20 × 10^(-2) m/s = 0.2 m/s
The moment of inertia for a solid disc is given by:
I=12mr2
Substituting the values:
I=12×100kg×(2m)2=12×100×4=200kg m2
The angular velocity can be calculated using the relation:
ω=vr
Substituting the values:
ω=0.2m/s2m=0.1rad/s
The total kinetic energy of the rolling disc is the sum of translational and rotational kinetic energy:
KEinitial=12Iω2+12mv2
Substituting the values:
KEinitial=12×200kg m2×(0.1rad/s)2+12×100kg×(0.2m/s)2
KEinitial=12×200×0.01+12×100×0.04
KEinitial=1+2=3J
Since the final kinetic energy (KE_final) when the disc is stopped is 0, the work done to stop the disc is equal to the initial kinetic energy:
W=KEfinal−KEinitial=0−3J=−3J
The work done to stop the disc is 3 J (the negative sign indicates that work is done against the motion).
The work needed to stop the disc is 3 joules.
Similar Questions
A hoop of radius 2m weight 100kg.It rolls along a horizontal floor so that its centre of mass has a speed of 20cms−1. How much work has to be done to stop it ?
View SolutionThe mass of a hoop of radius 0.30 m is 2kg. It rolls along a horizontal floor so that its centre of mass has a speed of 2 m/s. What is the work done to stop it ?
View Solution
Knowledge Check
A hoop of radius 2m weight 100kg.It rolls along a horizontal floor so that its centre of mass has a speed of 20cms−1. How much work has to be done to stop it ?
A2 JB4 JC6 JD8 J
A disc of radius R and mass m is projected on to a horizontal floor with a backward spin such that its centre of mass speed is v0 and angular velocity is ω0. What must be the minimum value of ω0 so that the disc eventually returns back?
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is

View Solution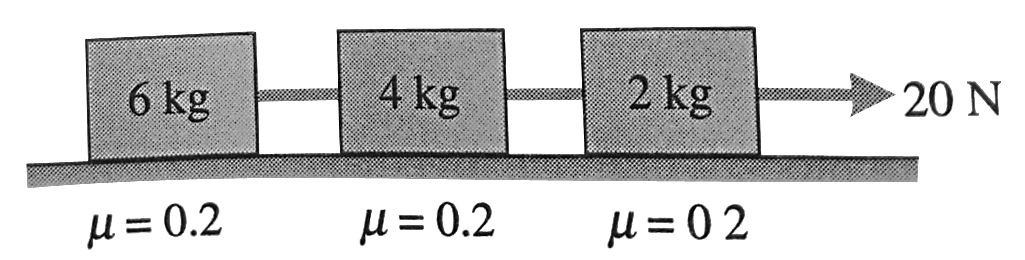
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View Solution
