If the velocity of a particle is v=At+Bt2, where A and B are constant, then the distance travelled by it between 1s and 2s is :
3A+7B
32A+73B
A2+B3
32A+4B
The correct Answer is:B
Step by step video & image solution for If the velocity of a particle is v = At + Bt^2, where A and B are constant, then the distance travelled by it between 1 s and 2 s is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
If xy=a2andS=b2x+c2y where a,bandc are constants then the minimum value of S is
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The total distance travelled by the paticle between t=0 to t=1s is
View SolutionThe variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
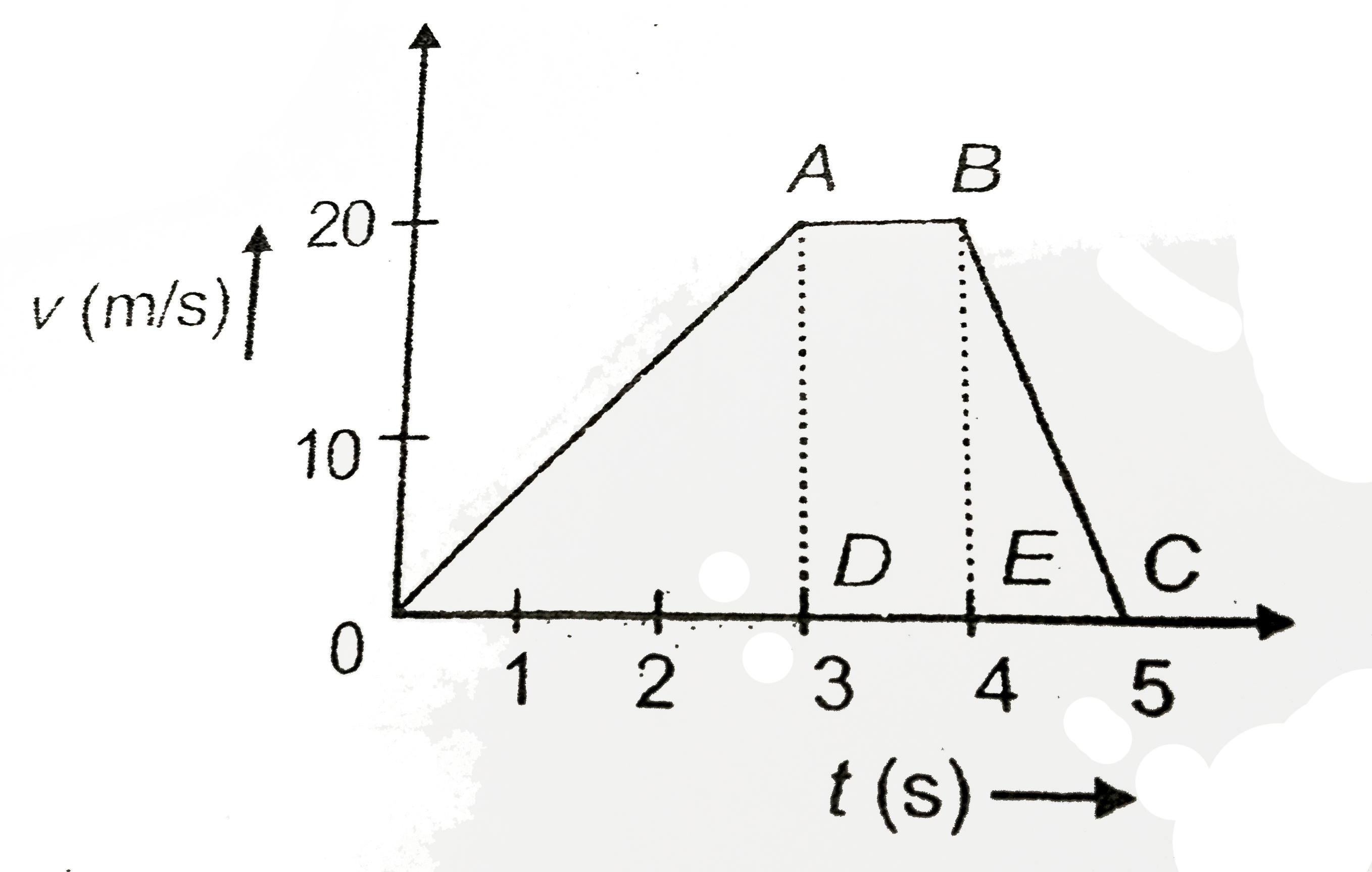
View SolutionThe position (in meters) of a particle moving on the x-axis is given by: x=2+9t+3t2−t3, where t is time in seconds . The distance travelled by the particle between t= 1s and t= 4s is m.
View SolutionThe momentum of a particle is P=A+Bt2 . Where , A and B are constant perpendicular vectors . The force acting on the particle when its acceleration is at 45∘ with its velocity is
(a)2√ABB (b)2B (c)zero (d)2A
View SolutionThe variation of velocity of a particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4s is
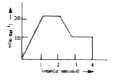
View SolutionThe period of a particle in SHM is 8s. At t=0 it is in its equilibrium position.
(a) Compare the distance travelled in the first 4s and the second 4s.
(b) Compare the distance travelled in the first 2s and the second 2s.
View SolutionIf velocity of a particle is given by v=(2t+3)m/s. Then average velocity in interval 0≤t≤1 s is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionVelocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View Solution
