Two cars P and Q start from a point at the same time in a straight line and their position are represented by xp(t)=at+bt2 and xQ(t)=ft−t2. At what time do the cars have the same velocity ?
a−f1+b
a+f2(b−1)
a+f2(1+b)
f−a2(1+b)
The correct Answer is:D
To find the time at which both cars P and Q have the same velocity, we will follow these steps:
Step 1: Write down the position functions
The position functions for the two cars are given as:
- For car P:
xP(t)=at+bt2
- For car Q:
xQ(t)=ft−t2
Step 2: Differentiate the position functions to find velocities
To find the velocities of both cars, we need to differentiate their position functions with respect to time t.
- The velocity of car P is:
vP(t)=dxPdt=ddt(at+bt2)=a+2bt
- The velocity of car Q is:
vQ(t)=dxQdt=ddt(ft−t2)=f−2t
Step 3: Set the velocities equal to find the time
We need to find the time t when both cars have the same velocity:
vP(t)=vQ(t)
Substituting the expressions we found:
a+2bt=f−2t
Step 4: Rearrange the equation
Rearranging the equation gives:
2bt+2t=f−a
Factoring out t from the left side:
t(2b+2)=f−a
Step 5: Solve for t
Now, we can solve for t:
t=f−a2(b+1)
Conclusion
Thus, the time at which both cars have the same velocity is:
t=f−a2(b+1)
The position functions for the two cars are given as:
- For car P:
xP(t)=at+bt2
- For car Q:
xQ(t)=ft−t2
To find the velocities of both cars, we need to differentiate their position functions with respect to time t.
vP(t)=dxPdt=ddt(at+bt2)=a+2bt
vQ(t)=dxQdt=ddt(ft−t2)=f−2t
We need to find the time t when both cars have the same velocity:
vP(t)=vQ(t)
Substituting the expressions we found:
a+2bt=f−2t
Rearranging the equation gives:
2bt+2t=f−a
Factoring out t from the left side:
t(2b+2)=f−a
Now, we can solve for t:
t=f−a2(b+1)
Thus, the time at which both cars have the same velocity is:
t=f−a2(b+1)
Similar Questions
Knowledge Check
A particle starts from point A moves along a straight line path with an acceleration given by a = p - qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
ApqBp√qCqpD√qp
Two cars, A and B move along the x-axis. Car A starts from rest with constant accelertion while car B moves with consstant velocity.
a. At what time s, t s, if any, do A and B have the same position?
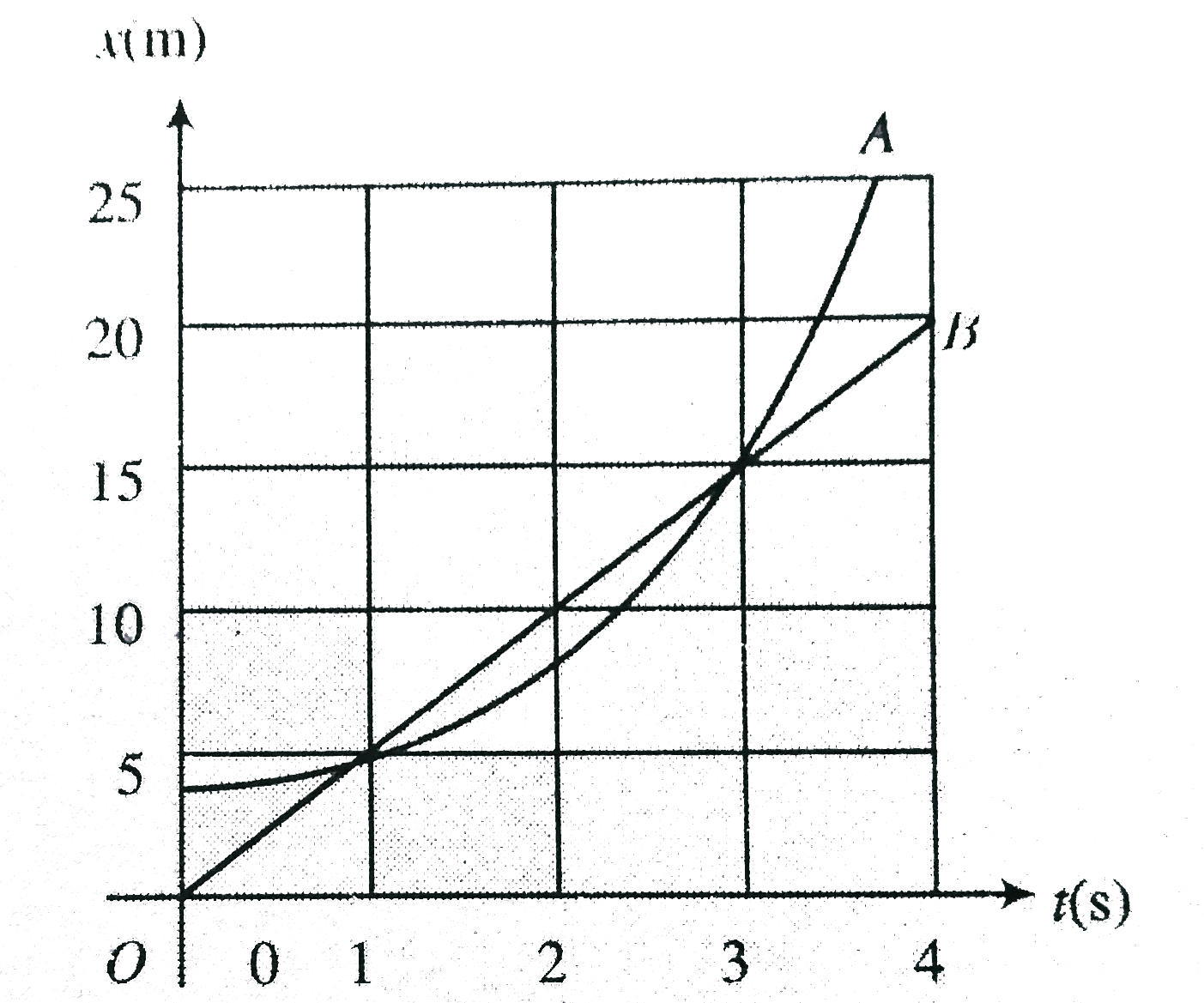 .
.
b. At what time s if any, do A and B have the same velocity? What is the velocity of car B at this time.
c. Graph velocity versus time for both A and B.
d. At what time s. If any, does car ApasscarA?<br>e.Atwˆtimes,ifanydoescarBpasscarA?
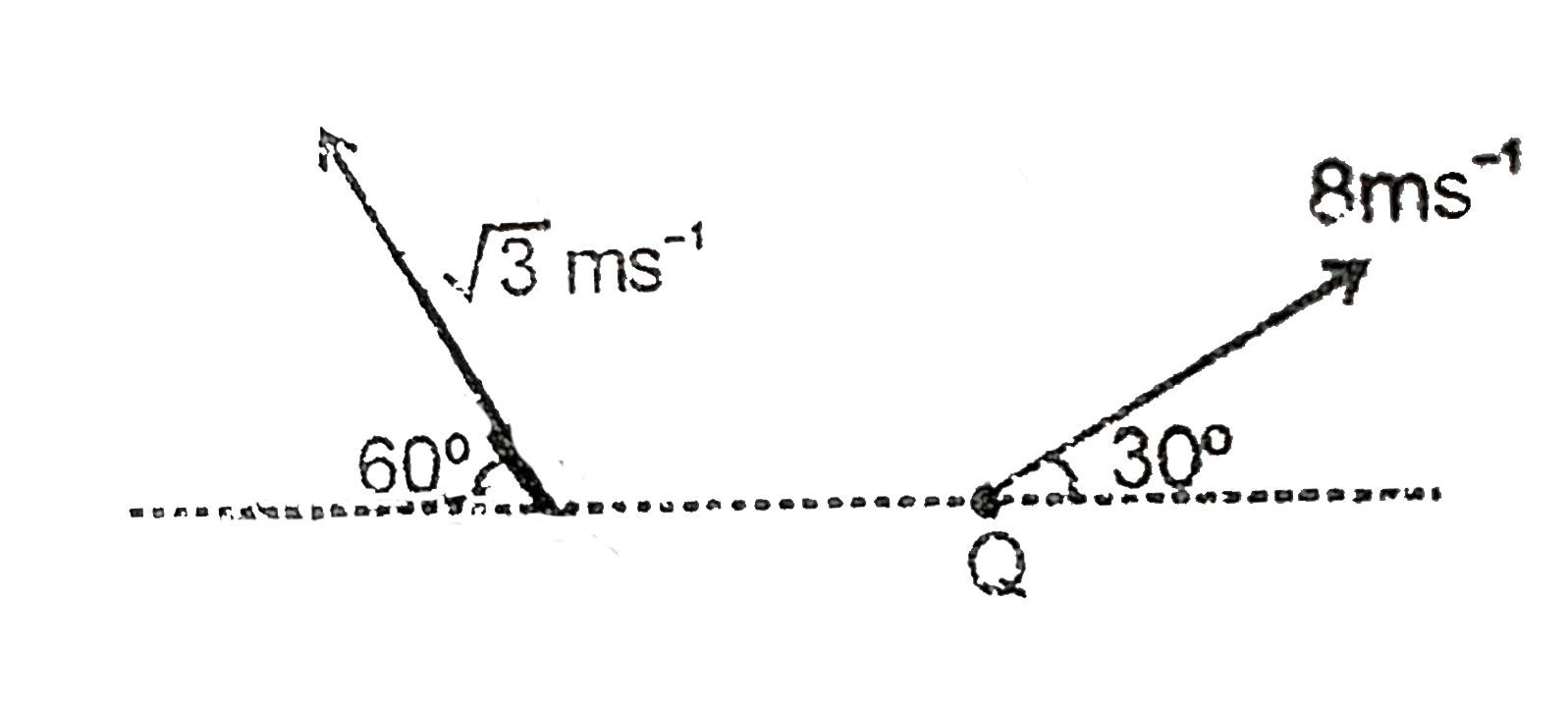
View SolutionTwo particles P and Q are moving as shown in the figure. At this moment of time the angular speed of P w.r.t. Q is
View SolutionTwo cars start in a race with velocities u1 and u2 and travel in a straight line with acceleration 'a' and b .If both reach the finish line at the same time,the range of the race is
View SolutionA particle is thrown vertically upwards from the surface of the earth. Let TP be the time taken by the particle to travel from a point P above the earth to its highest point and back to the point P. Similarly, let TQ be the time taken by the particle to travel from another point Q above the earth to its highest point and back to the same in terms of TP,TQ and H, is :-
View SolutionA point mives in a straight line so its displacement x mertre at time t second is given by x2=1+t2. Its aceleration in ms−2 at time t second is .
View SolutionFor a particle moving along a straight line, the displacement x depends on time t as x=αt3+βt2+γt+δ. The ratio of its initial acceleration to its initial velocity depends
View SolutionA car starts from a point P at time t = 0 seconds and stops at point Q. The distance x, in metres, covered by it, in t seconds is given by x=t2(2−t3)Find the time taken by it to reach Q and also find distance between P and Q.
View Solution