A body of mass 1kg is thrown upwards with a velocity 20ms−1. It momentarily comes to rest after attaining a height of 18m. How much energy is lost due to air friction? (g=10ms−2)
20J
30J
40J
10J
The correct Answer is:a
To solve the problem, we will use the principle of conservation of energy. The total mechanical energy of the body when it is thrown upwards is converted into potential energy at the maximum height it reaches. However, some energy is lost due to air friction.
Step 1: Calculate the initial kinetic energy (KE_initial)
The initial kinetic energy when the body is thrown upwards can be calculated using the formula:
KEinitial=12mv2
Where:
- m=1kg (mass of the body)
- v=20m/s (initial velocity)
Substituting the values:
KEinitial=12×1×(20)2=12×1×400=200J
Step 2: Calculate the final potential energy (PE_final)
The potential energy at the maximum height can be calculated using the formula:
PEfinal=mgh
Where:
- g=10m/s2 (acceleration due to gravity)
- h=18m (maximum height)
Substituting the values:
PEfinal=1×10×18=180J
Step 3: Calculate the energy lost due to air friction
The energy lost due to air friction can be found by taking the difference between the initial kinetic energy and the final potential energy:
Energy lost=KEinitial−PEfinal
Substituting the values we calculated:
Energy lost=200J−180J=20J
Final Answer
The energy lost due to air friction is 20 Joules.
---
The initial kinetic energy when the body is thrown upwards can be calculated using the formula:
KEinitial=12mv2
Where:
- m=1kg (mass of the body)
- v=20m/s (initial velocity)
KEinitial=12×1×(20)2=12×1×400=200J
The potential energy at the maximum height can be calculated using the formula:
PEfinal=mgh
Where:
- g=10m/s2 (acceleration due to gravity)
- h=18m (maximum height)
PEfinal=1×10×18=180J
The energy lost due to air friction can be found by taking the difference between the initial kinetic energy and the final potential energy:
Energy lost=KEinitial−PEfinal
Substituting the values we calculated:
Energy lost=200J−180J=20J
The energy lost due to air friction is 20 Joules.
Similar Questions
A body of mass 10 kg initially at rest acquires velocity 10ms−1. What is the work done ?
View SolutionA particle of mass 2 kg is projected vertically upward with a velocity of 20 m/s. It attains maximum height of 17 m. The loss in mechanical energy due to air drag is (g=10ms−2)
View SolutionA body of mass 500 g is thrown upwards with a velocity 20ms−1 and reaches back to the surface of a planet after 20sec. Then the weight of the body on that planet is (Assume g to be constant) xN. Find x.
View SolutionA stone of mass 1 kg is thrown with a velocity of 20ms−1 across the frozen surface of a lake and it comes to rest after travelling a distance of 50m. What is the magnitude of the force opposing the motion of the stone?
View SolutionA stone of 1kg is thrown with a velocity of 20ms−1 across the frozen surface of lake and comes to rest after travelling a distance of 50m. What is the force of friction between the stone and the ice?
View SolutionA body is thrown up with a velocity 29.23ms−1 distance travelled in last second of upward motion is
View SolutionIf a stone is thrown up with a velocity of 9.8ms−1, then how much time will it take to come back ?
View SolutionA particle of mass 1 kg is projected upwards with velocity 60ms−1. Another particle of mass 2kg is just dropped from a certain height. After 2s, match the following.
[Take, g =10ms−2]
column1column2Accelertion of CMP ZeroB Velocity of CMQ 10 SI unitC Displacement of CMR 20 SI unit-S None
View SolutionA stone is thrown vertically up from a bridge with velocity 3ms−1. If it strikes the water under the bridge after 2 s, the bridge is at a height of (g=10ms−2)
View SolutionA light inelastic thread passes over a small frictionless pulley. Two blocks of masses m = 1 kg and M = 3 kg, respectively, are attached with the thread and heavy block rests on a surface. A particle P of mass 1 kg moving upward with a velocity of 10ms−1 collides with the lighter block and sticks to it. The speed of the bigger block just after the string is taut will be [g=10ms−2]
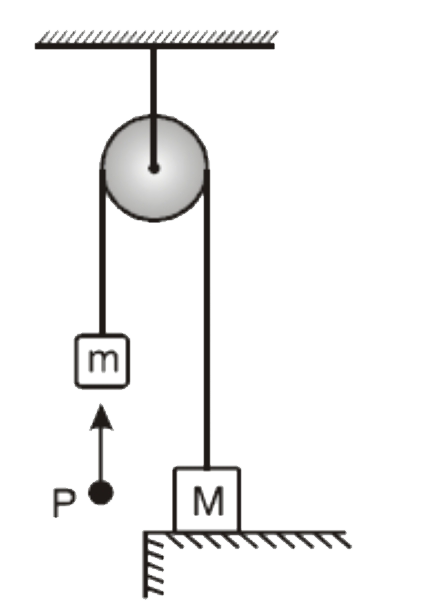
View Solution
