The KE acquired by a mass m in travelling a certain distance s, starting from rest, under the action of a constant force is directly proportional to :
m
√m
1√m
independent m
The correct Answer is:d
To solve the problem, we need to determine the relationship between the kinetic energy (KE) acquired by a mass m traveling a distance s under a constant force, starting from rest.
1. Understanding the Initial Conditions:
- The mass m starts from rest, which means the initial velocity u=0.
2. Using the Kinematic Equation:
- We can use the kinematic equation to relate the final velocity v to the distance s traveled under constant acceleration a:
v2=u2+2as
- Since u=0, this simplifies to:
v2=2as
3. Relating Acceleration to Force:
- According to Newton's second law, the acceleration a can be expressed as:
a=Fm
- Here, F is the constant force acting on the mass.
4. Substituting Acceleration into the Velocity Equation:
- Substitute a into the equation for v2:
v2=2(Fm)s
5. Calculating Kinetic Energy:
- The kinetic energy KE is given by:
KE=12mv2
- Substitute v2 from the previous step into the kinetic energy formula:
KE=12m(2Fms)
- Simplifying this gives:
KE=12⋅2⋅F⋅s=F⋅s
6. Conclusion:
- From the final expression, we see that the kinetic energy KE is directly proportional to the force F and the distance s, but it is independent of the mass m.
Final Answer:
The kinetic energy acquired by a mass m in traveling a certain distance s under the action of a constant force is directly proportional to the distance s and the force F, but not to the mass m.
- The mass m starts from rest, which means the initial velocity u=0.
- We can use the kinematic equation to relate the final velocity v to the distance s traveled under constant acceleration a:
v2=u2+2as
- Since u=0, this simplifies to:
v2=2as
- According to Newton's second law, the acceleration a can be expressed as:
a=Fm
- Here, F is the constant force acting on the mass.
- Substitute a into the equation for v2:
v2=2(Fm)s
- The kinetic energy KE is given by:
KE=12mv2
- Substitute v2 from the previous step into the kinetic energy formula:
KE=12m(2Fms)
- Simplifying this gives:
KE=12⋅2⋅F⋅s=F⋅s
- From the final expression, we see that the kinetic energy KE is directly proportional to the force F and the distance s, but it is independent of the mass m.
The kinetic energy acquired by a mass m in traveling a certain distance s under the action of a constant force is directly proportional to the distance s and the force F, but not to the mass m.
Similar Questions
The K.E. acquired by a mass m in travelling a certain distance d, starting from rest, under the action of a constant force is directly propotional to
View SolutionThe velocity acquired by a mass m in travelling a certain distance d starting from rest under the action of a constant force is directly proportional to :-
View Solution
Knowledge Check
The kinetic energy acquired by a mass m after travelling a fixed distance from rest under the action of constant force is
Adirectly proportional √mBinversely proportional to √mCdirectly proportional to m.Dindependent of m.A particle of mass 0.1 kg is subjected to a force which is directly proportional to the distance x. the work done by the force is directly proportional to
AxBx3Cx3/2Dx2
The kinetic energy acquired by a mass m travelling a certain distance d, starting from rest, under the action of a force F such that the force F is directly proportional to t is
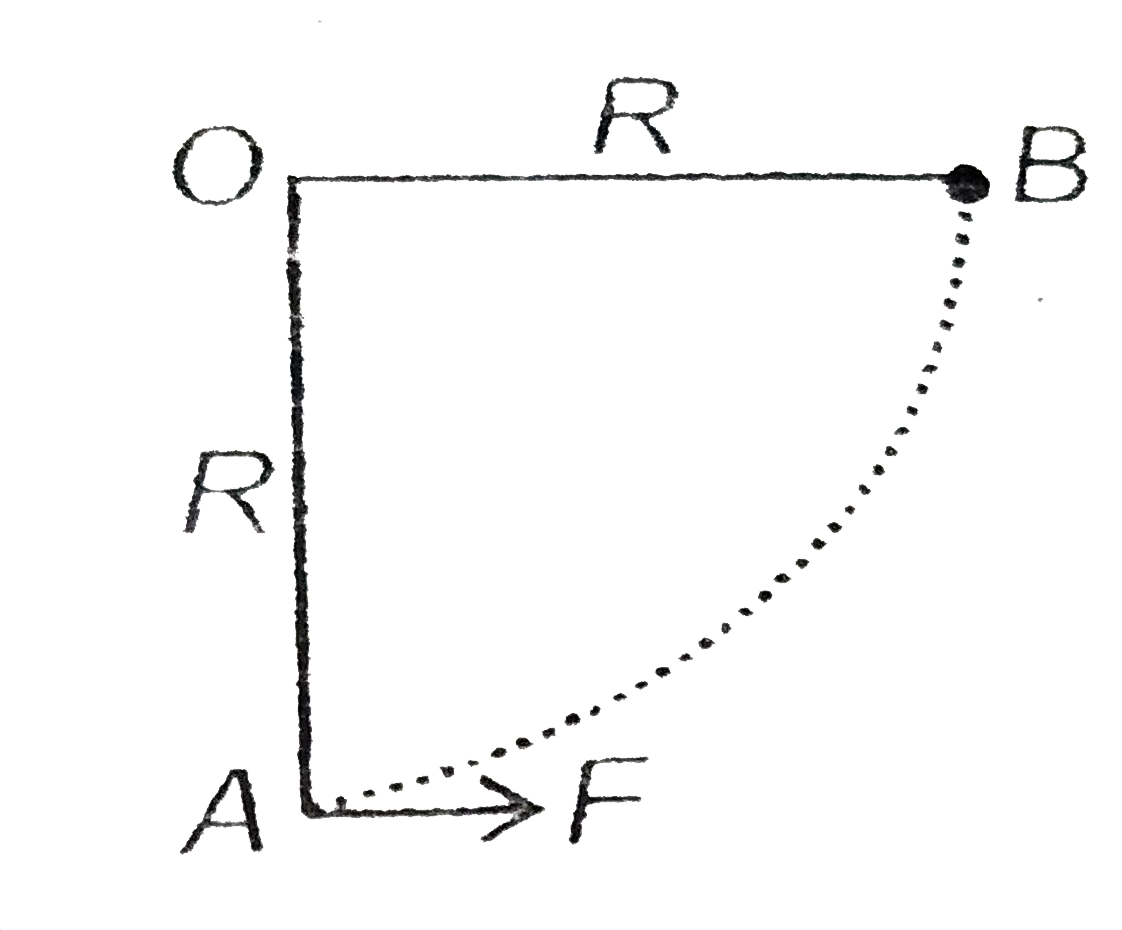
View SolutionA block of mass m is taken from A to B under the action of a constant force F. Work done by this force is
View SolutionA particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
View SolutionA constant force acts on a mass m at rest. Velocity acquired in travelling a fixed distance is directly proportional to :
View SolutionA uniform square plate of mass m and edge a initially at rest startas rotating about one of the edge under the action of a constant torque τ. Then at the end of the 5th sec after start
View SolutionEngine of car of mass m supplies a constant power P. Starting from rest at an instant of time, then
View Solution
