The instantaneous angular position of a point on a rotating wheel is given by the equation
θ(t)=2t3−6t2
The torque on the wheel becomes zero at
t=0.5s
t=0.25s
t=2s
t=1s
The correct Answer is:d
To find the time at which the torque on the wheel becomes zero, we need to follow these steps:
Step 1: Understand the relationship between torque and angular acceleration
Torque (τ) is given by the equation:
τ=I⋅α
where I is the moment of inertia and α is the angular acceleration. For the torque to be zero, we need α=0 since the moment of inertia I cannot be zero.
Step 2: Find the angular acceleration
The angular acceleration α is the second derivative of the angular position θ(t) with respect to time t:
α=d2θdt2
Given the angular position:
θ(t)=2t3−6t2
Step 3: Differentiate the angular position to find the first derivative (angular velocity)
First, we differentiate θ(t) with respect to time t:
dθdt=ddt(2t3−6t2)=6t2−12t
Step 4: Differentiate again to find the angular acceleration
Now, we differentiate the angular velocity to find the angular acceleration:
α=d2θdt2=ddt(6t2−12t)=12t−12
Step 5: Set the angular acceleration to zero
To find when the torque is zero, we set the angular acceleration α to zero:
12t−12=0
Step 6: Solve for t
Now, we solve for t:
12t=12⟹t=1 second
Conclusion
The torque on the wheel becomes zero at t=1 second.
---
Torque (τ) is given by the equation:
τ=I⋅α
where I is the moment of inertia and α is the angular acceleration. For the torque to be zero, we need α=0 since the moment of inertia I cannot be zero.
The angular acceleration α is the second derivative of the angular position θ(t) with respect to time t:
α=d2θdt2
Given the angular position:
θ(t)=2t3−6t2
First, we differentiate θ(t) with respect to time t:
dθdt=ddt(2t3−6t2)=6t2−12t
Now, we differentiate the angular velocity to find the angular acceleration:
α=d2θdt2=ddt(6t2−12t)=12t−12
To find when the torque is zero, we set the angular acceleration α to zero:
12t−12=0
Now, we solve for t:
12t=12⟹t=1 second
The torque on the wheel becomes zero at t=1 second.
Similar Questions
The angular position of a point over a rotating flywheel is changing according to the relation, θ=(2t3−3t2−4t−5) radian. The angular acceleration of the flywheel at time, t = 1 s is
View SolutionA boat of mass 300 kg moves according to the equation x=1.2t2−0.2t3. When the force will become zero ?
View SolutionA angular positio of a point on the rim of a rotating wheel is given by θ=4t−3t2+t3 where θ is in radiuans and t is in seconds. What are the angualr velocities at
(a).t=2.0 and
(b). t=4.0s
(c). What is the average angular acceleration for the time interval that begins at t=2.0s and ends at t=4.0s?
(d). What are the instantaneous angular acceleration at the biginning and the end of this time interval?
View SolutionThe position of a particle is given by the equation f(t)=t3−6t2+9t where t is measured in second and s in meter. Find the acceleration at time t. What is the acceleration at 4 s?
View SolutionThe position of a particle moving along x-axis given by x=(−2t3−3t2+5)m. The acceleration of particle at the instant its velocity becomes zero is
View SolutionThe variation of angular position θ, of a point on a rotating rigid body, with time t is shown in Fig. Is the body rotating clock wise or anti-clockwise ?
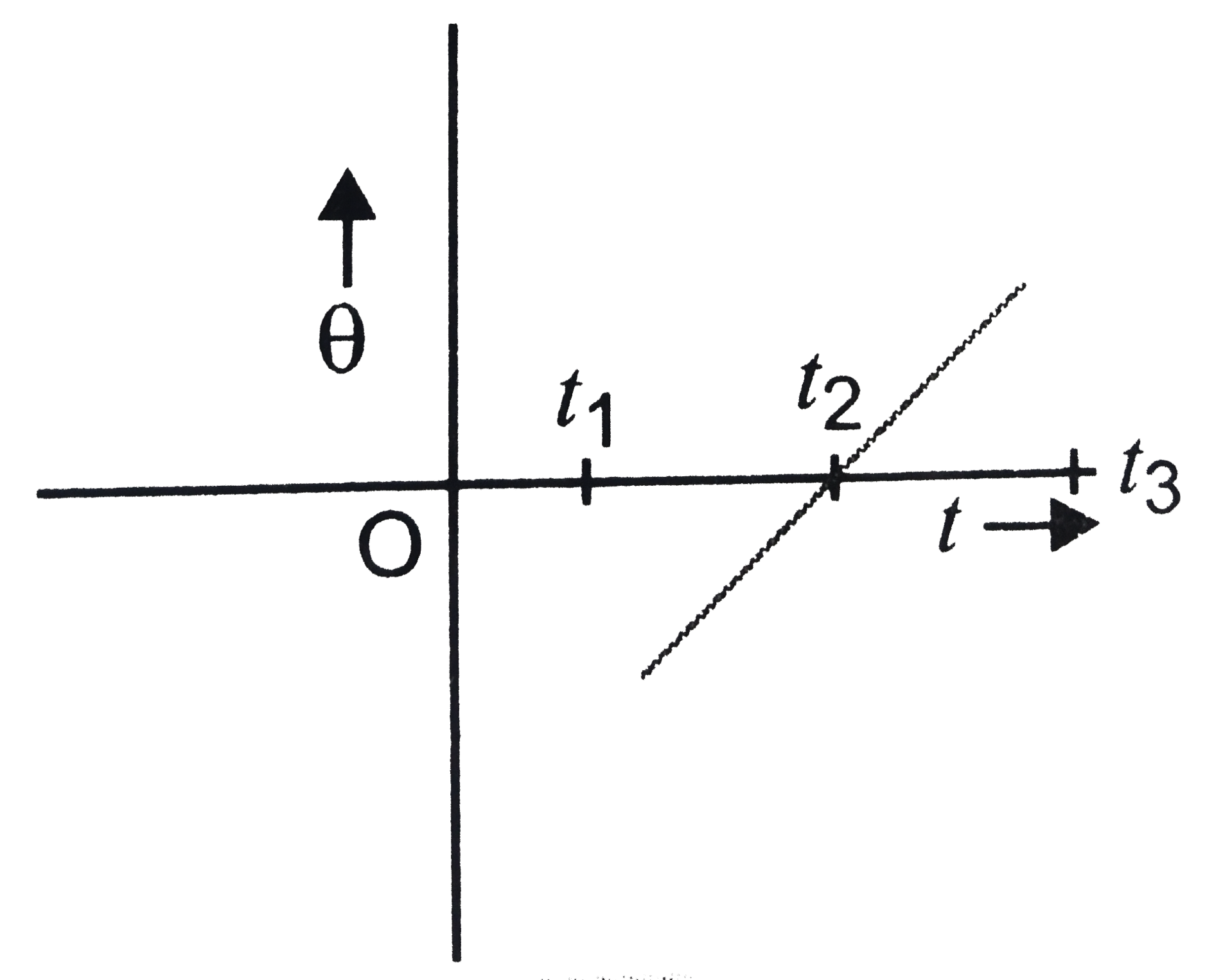
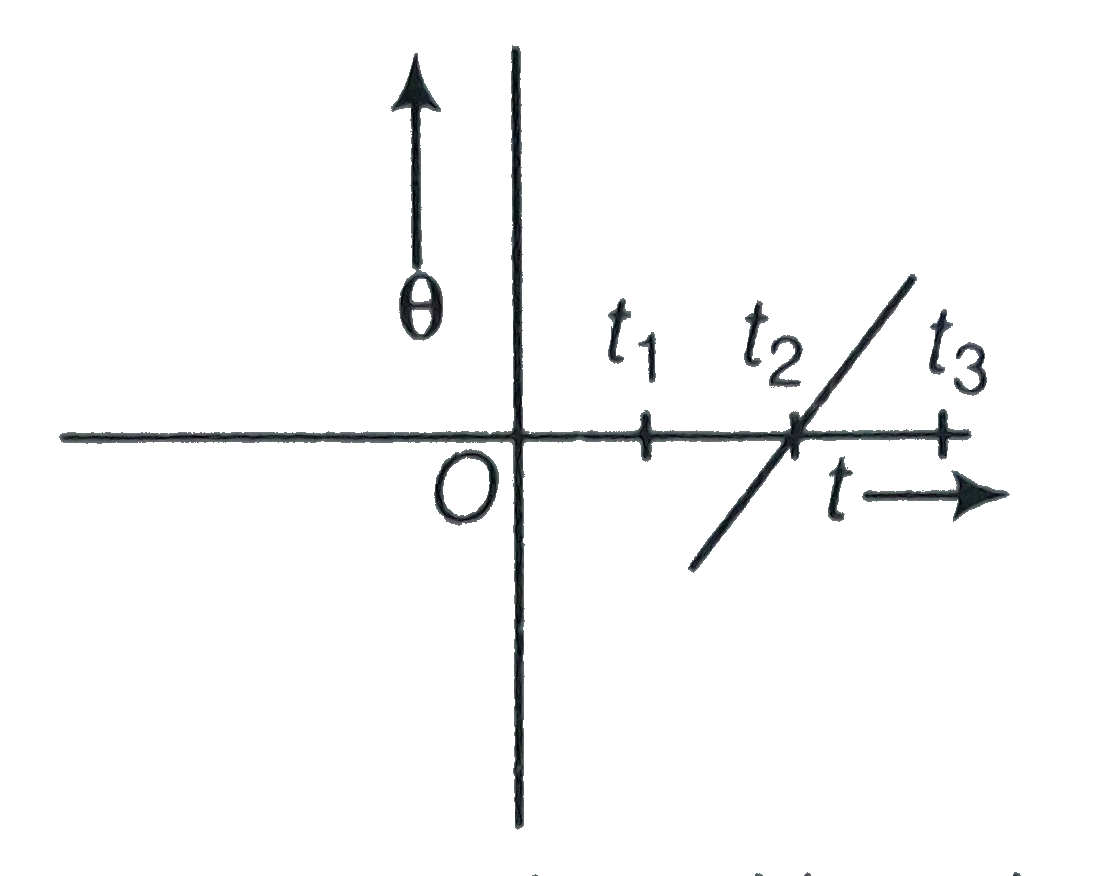
View Solutionthe variaton of angular postion θ of a point on a rotating rigid body with time t is shown in figure Is the body rotating clokwise or anti- clokwise ?
View SolutionThe displacement of a particle moving along the x-axis is given by equation x=2t3−21t2+60t+6.The possible acceleration of the particle when its velocity is zero is
View SolutionThe angular position of a line of a disc of radius r = 6cm is given by θ=10−5t+4t2 rad , the average angular velocity between 1 and 3s is
View SolutionThe velocity of an object is changing with time and relation is given by the following equation.
v=2t+3t2
Calculate the position of the object from the origin at t = 2 s.
Assume particle to be at origin at t = 0
View Solution
