A black hole is an object whose gravitational field is so strong that even light cannot escape from it. To what approximate radius would earth (mass =5.98×1024kg) have to be compresed to be a black hole?
10−9m
10−6m
10−2m
100m
The correct Answer is:C
To determine the radius to which Earth must be compressed to become a black hole, we need to find the Schwarzschild radius (the radius of a black hole) using the escape velocity formula. Here’s the step-by-step solution:
Step 1: Understand the concept of escape velocity
The escape velocity v from the surface of a mass M at a distance r is given by the formula:
v=√2GMr
where G is the gravitational constant, approximately 6.67×10−11m3/kg⋅s2.
Step 2: Set the escape velocity equal to the speed of light
For Earth to become a black hole, the escape velocity must equal the speed of light c:
c=3×108m/s
Thus, we set:
3×108=√2GMr
Step 3: Square both sides of the equation
Squaring both sides to eliminate the square root gives:
(3×108)2=2GMr
Calculating (3×108)2:
9×1016=2GMr
Step 4: Rearrange the equation to solve for r
Rearranging the equation to isolate r:
r=2GM9×1016
Step 5: Substitute the known values
Substituting G=6.67×10−11m3/kg⋅s2 and M=5.98×1024kg:
r=2×(6.67×10−11)×(5.98×1024)9×1016
Step 6: Calculate the numerator
Calculating the numerator:
2×6.67×5.98≈79.76(approximately)
Thus, the numerator becomes:
79.76×1013(since 10−11×1024=1013)
Step 7: Calculate r
Now substituting back:
r=79.76×10139×1016=79.769×10−3
Calculating 79.769:
≈8.86(approximately)
Thus:
r≈8.86×10−3m
Step 8: Final approximation
The approximate radius to which Earth must be compressed to become a black hole is:
r≈8.86×10−3m≈10−2m
Conclusion
Therefore, the answer is approximately 10−2m.
---
The escape velocity v from the surface of a mass M at a distance r is given by the formula:
v=√2GMr
where G is the gravitational constant, approximately 6.67×10−11m3/kg⋅s2.
For Earth to become a black hole, the escape velocity must equal the speed of light c:
c=3×108m/s
Thus, we set:
3×108=√2GMr
Squaring both sides to eliminate the square root gives:
(3×108)2=2GMr
Calculating (3×108)2:
9×1016=2GMr
Rearranging the equation to isolate r:
r=2GM9×1016
Substituting G=6.67×10−11m3/kg⋅s2 and M=5.98×1024kg:
r=2×(6.67×10−11)×(5.98×1024)9×1016
Calculating the numerator:
2×6.67×5.98≈79.76(approximately)
Thus, the numerator becomes:
79.76×1013(since 10−11×1024=1013)
Now substituting back:
r=79.76×10139×1016=79.769×10−3
Calculating 79.769:
≈8.86(approximately)
Thus:
r≈8.86×10−3m
The approximate radius to which Earth must be compressed to become a black hole is:
r≈8.86×10−3m≈10−2m
Therefore, the answer is approximately 10−2m.
Similar Questions
Find the distance of a point from the earth's centre where the resultant gravitational field due to the earth and the moon is zero. The mass of the earth is 6.0×1024 kg and that of the moon is 7.4x1022 kg. The distance between the earth and the moon is 4.0×105km.
View SolutionWhat is the magnitude of the gravitational force between the Earth and a 1kg object on its surface ? (Mass of the earth is 6×1024 kg and radius of the Earth is 6.4×106m).
View SolutionFind the distance of a point from the earth's centre where the resultant gravitational field due to the earth and the moon is zero The mass of the earth is 6.0×1024kg and that of the moon is 7.4×1022kg The distance between the earth and the moon is 4.0×105km .
View SolutionWhat would be the escape velocity from the moon, it the mass of the moon is 7.4×1022 kg and its radius is 1740 km ?
View SolutionLet the sun contracts due to self-gravity and it becomes a black hole. If the mass of sun is 2x1030 kg, then possible radius of sun to behave as a black hole is
View SolutionWhat should be the radius of a planet with mass equal to that of earth and escape velocity on its surface is equal to the velocity of light. Given that mass of earth is M=6×1024kg.
View SolutionCalculate the orbital speed of the Hubble space telescope orbiting at a height of 598 km above the earth's surface. Take R = 6400km. Mass of earth −5.98×1024kg
View SolutionThe earth circles the sun once a year. How much work would have to be done on the earth to bring it to rest relative to the sun, (ignore the rotation of earth about - its own axis) Given that mass of the earth is 6×1024 kg and distance between the sun and earth is 1.5×108 km-
View SolutionThe mass of one steel screw is 4.11 g. Find the mass of the of one mole of these steel screws. Compare this value with the mass of the earth (5.98×1024kg). Which one of the two is heavier and by how many times?
View SolutionAn unmanned satellite A and a spacecraft B are orbiting around the earth in the same circular orbit as shown.
 The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
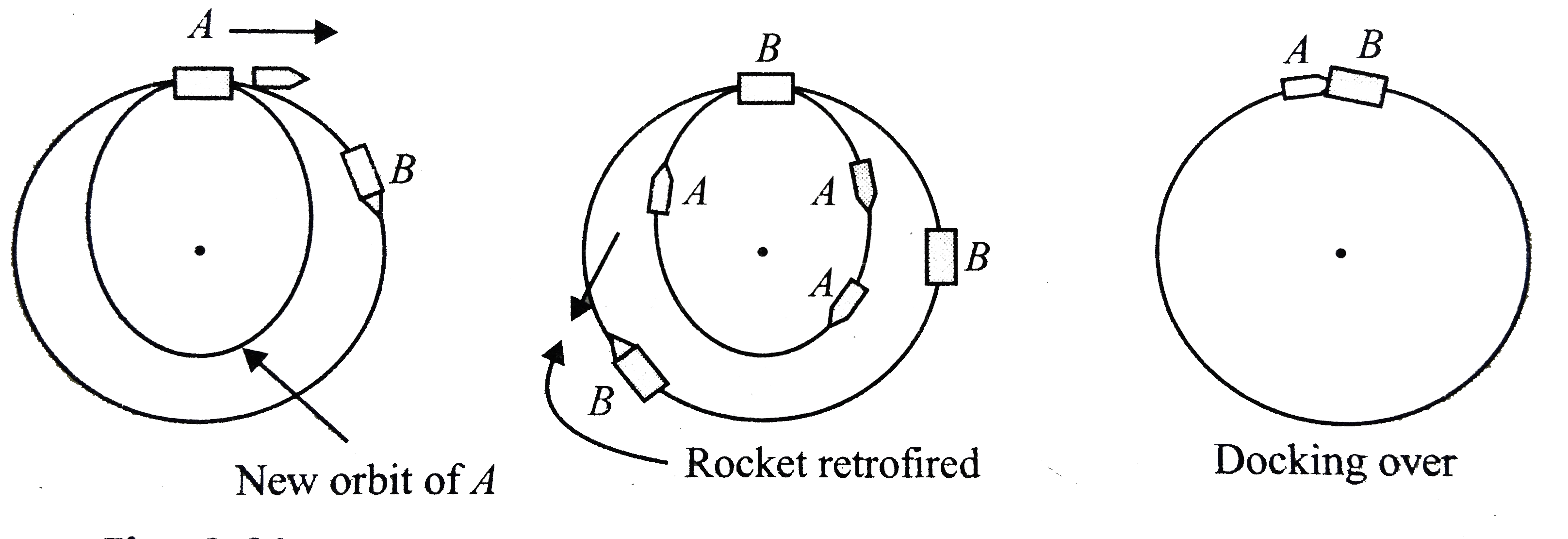
Take mass of the earth =5.98×1024kg
Radius of the earth =6400km
Orbital radius =9600km
Mass of satellite A=320kg
Mass of spacecraft =3200kg
Assume that initially spacecraft B leads satellite A by 100s, i.e., A arrives at any particle position after 100s of B’s arrival. Based on the above information answer the following questions
The initial total energy and time period of satellite are, respectively,
View Solution
