A body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1kg, the time period of oscillations becomes 5s. The value of m in kg is
34kg
43kg
169kg
916kg
The correct Answer is:D
To solve the problem, we will use the formula for the time period of oscillation of a mass-spring system, which is given by:
T=2π√mk
where T is the time period, m is the mass attached to the spring, and k is the spring constant.
Step 1: Set up equations for the two cases
1. For the first case (mass m and time period T1=3s):
T1=2π√mk(1)
2. For the second case (mass m+1kg and time period T2=5s):
T2=2π√m+1k(2)
Step 2: Square both equations to eliminate the square root
1. From equation (1):
T21=(2π)2mk⟹9=4π2mk
Rearranging gives:
mk=94π2(3)
2. From equation (2):
T22=(2π)2m+1k⟹25=4π2m+1k
Rearranging gives:
m+1k=254π2(4)
Step 3: Set up a system of equations using (3) and (4)
From equations (3) and (4), we can express m+1k in terms of mk:
m+1k=mk+1k
Substituting the values from equations (3) and (4):
254π2=94π2+1k
Step 4: Solve for 1k
Rearranging gives:
1k=254π2−94π2=164π2=4π2
Step 5: Substitute back to find m
Now substitute 1k back into equation (3):
mk=94π2⟹m=94π2⋅k
Substituting k=4π2:
m=94π2⋅4π2=9π4
Step 6: Calculate m
Using π≈3.14:
m≈9(3.14)2≈99.8596≈0.91kg
Final Answer
The value of m is approximately 0.91kg.
T1=2π√mk(1)
T2=2π√m+1k(2)
T21=(2π)2mk⟹9=4π2mk
Rearranging gives:
mk=94π2(3)
T22=(2π)2m+1k⟹25=4π2m+1k
Rearranging gives:
m+1k=254π2(4)
m+1k=mk+1k
Substituting the values from equations (3) and (4):
254π2=94π2+1k
1k=254π2−94π2=164π2=4π2
mk=94π2⟹m=94π2⋅k
Substituting k=4π2:
m=94π2⋅4π2=9π4
m≈9(3.14)2≈99.8596≈0.91kg
Similar Questions
A body of mass m is atteched to the lower end of a spring whose upper end is fixed .The spring has negaligible mass .When the mass m is slightly puylled down and released it oscillation with a time period of 3s when the mass m is increased by 1kg time period of oscillations becomes 5s The value of m in kg is
View SolutionA body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
View SolutionThe time period of small oscillations of mass m :-
_S01_040_Q01.png)
View SolutionA body of mass m attached to a spring which is oscillating with time period 4 s. If the mass of the body is increased by 4 kg, its time period increases by 2 s. Determine value of initial mass m.
View SolutionA mass M is suspended from a spring of negligible mass. The spring is pulled a little then released, so that the mass executes simple harmonic motion of time period T. If the mass is increased by m, the time period becomes 5T3. Find the ratio of m/M.
View SolutionWhen a mass m attached to a spring it oscillates with period 4s. When an additional mass of 2 kg is attached to a spring, time period increases by 1s. The value of m is :-
View SolutionA mass M, attached to a spring, oscillates with a period of 2s. If the mass is increased by 4kg, the time period increases by one second. Assuming that Hooke's law is obeyed, find the initial mass M.
View SolutionA mass M is suspended from a spring of negiliglible mass the spring is pulled a little and then released so that the mass executes simple harmonic oscillation with a time period T If the mass is increases by m the time period because (54T),The ratio of mM is
View Solution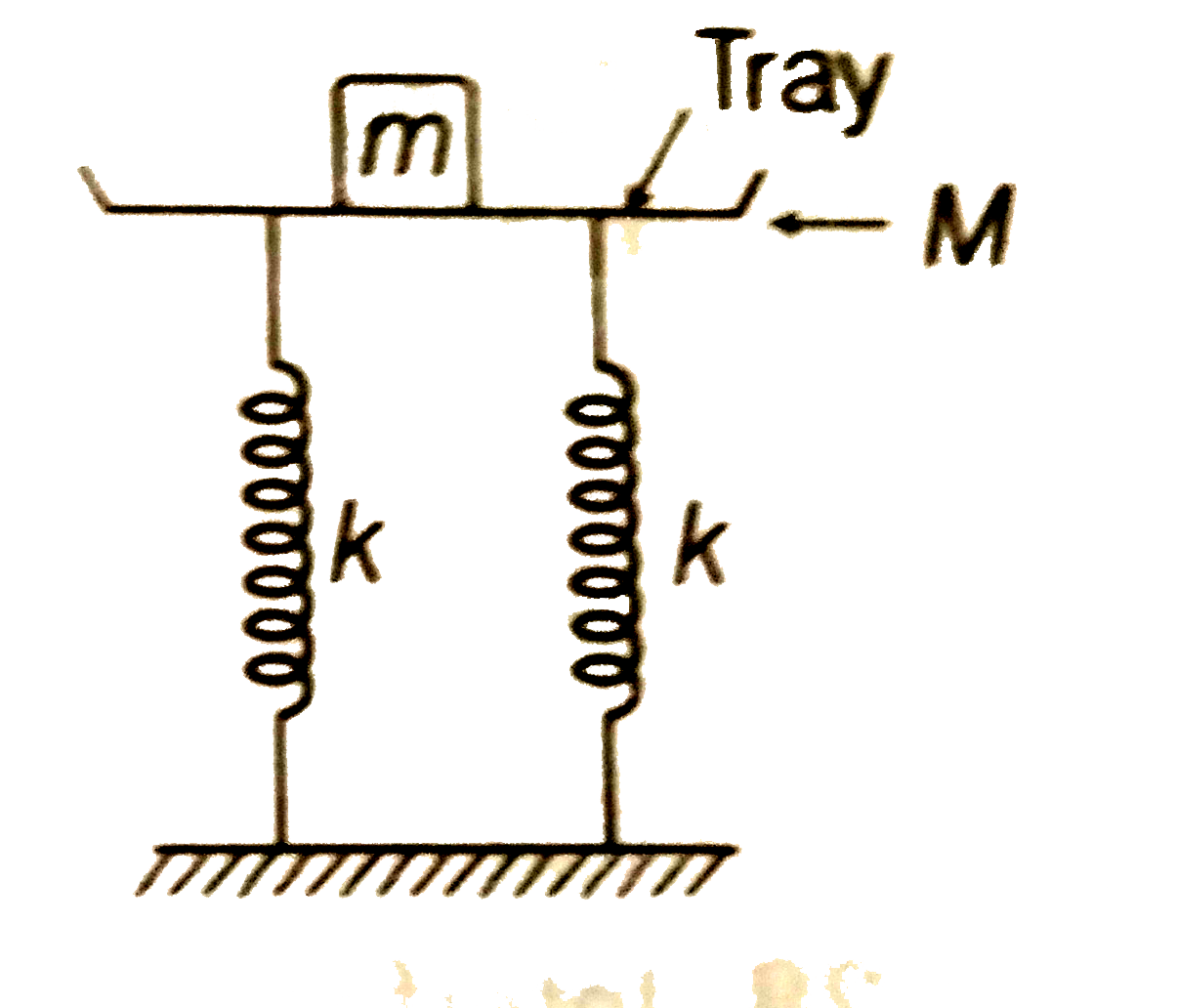
A tray of mass M=10kg is supported on two identical springs, each of spring constant k, as shown in figure, when the tray is depressed a little and released, it executes simple harmonic motion of period 1.5 s. when a block of mass m is placed on the tray, the speed of oscillation becomes 3 s. the value of m is
View SolutionA mass M attached to a spring oscillation with a period of 2s. If the mass is increased by 2kg , the period increases by 1s, find the initial mass m assuming that Hooke's law is obeyed.
View Solution