A bullet of mass 2gm is having a charge of 2μc. Through what potential difference must it be accelerated, starting from rest, to acquire a speed of 10m/s
(a) 5kV
(b) 50kV
(c) 5V
(d) 50V
5kV
50kV
5V
50V
The correct Answer is:B
To solve the problem, we need to find the potential difference required to accelerate a bullet of mass 2 grams and charge 2 microcoulombs to a speed of 10 m/s. We will use the relationship between kinetic energy and electric potential energy.
1. Convert the mass from grams to kilograms:
Mass(m)=2grams=2×10−3kg
Hint: Remember that 1 gram = 0.001 kg.
2. Convert the charge from microcoulombs to coulombs:
Charge(Q)=2μC=2×10−6C
Hint: Recall that 1 microcoulomb (μC) = 10−6 coulombs.
3. Use the formula for kinetic energy (KE):
The kinetic energy of the bullet when it reaches a speed v is given by:
KE=12mv2
Substituting the values:
KE=12×(2×10−3)×(10)2
KE=12×(2×10−3)×100=0.1J
Hint: Remember to square the velocity and multiply by half the mass.
4. Relate kinetic energy to electric potential energy:
The change in electric potential energy (PE) when the charge is accelerated through a potential difference V is given by:
PE=QV
Setting the change in kinetic energy equal to the change in potential energy:
QV=KE
Therefore, we can express the potential difference V as:
V=KEQ
Hint: This step uses the principle of conservation of energy.
5. Substituting the values to find the potential difference:
V=0.1J2×10−6C
V=0.12×10−6=5×104V=50kV
Hint: When dividing, ensure to handle the powers of ten correctly.
6. Final Answer:
The potential difference required is:
V=50kV
Thus, the correct option is (b) 50kV.
Mass(m)=2grams=2×10−3kg
Charge(Q)=2μC=2×10−6C
The kinetic energy of the bullet when it reaches a speed v is given by:
KE=12mv2
Substituting the values:
KE=12×(2×10−3)×(10)2
KE=12×(2×10−3)×100=0.1J
The change in electric potential energy (PE) when the charge is accelerated through a potential difference V is given by:
PE=QV
Setting the change in kinetic energy equal to the change in potential energy:
QV=KE
Therefore, we can express the potential difference V as:
V=KEQ
V=0.1J2×10−6C
V=0.12×10−6=5×104V=50kV
The potential difference required is:
V=50kV
Similar Questions
A mass of 1kg carrying a charge of 2C is accelerated through a potential of 1V. The velocity acquired by it is
View SolutionWhat amount of work of work in needed in moving 2C Charge through a potential difference of 8V.
View SolutionAn electron of mass m and charge e is accelerated from rest through a potential difference V in vacuum. The final speed of the electron will be
View SolutionAn electron of mass m and charge e is accelerated from rest through a potential difference V in vacuum. The final speed of the electron will be
View SolutionA particle of charges Q and mass m travels through a potential difference V from rest. The final momentum of the particle is
View SolutionThe kinetic energy of an electron accelerated from rest through a potential difference of 50V will be:
View SolutionThe kinetic energy of an electron accelerated from rest through a potential difference of 5V will be:
View SolutionThe kinetic energy of an electron accelerated from rest through a potential difference of 10V will be:
View SolutionFigure shows two rings having charges Q and −√5Q. Find potential difference a and B i.e. (VA−VB).
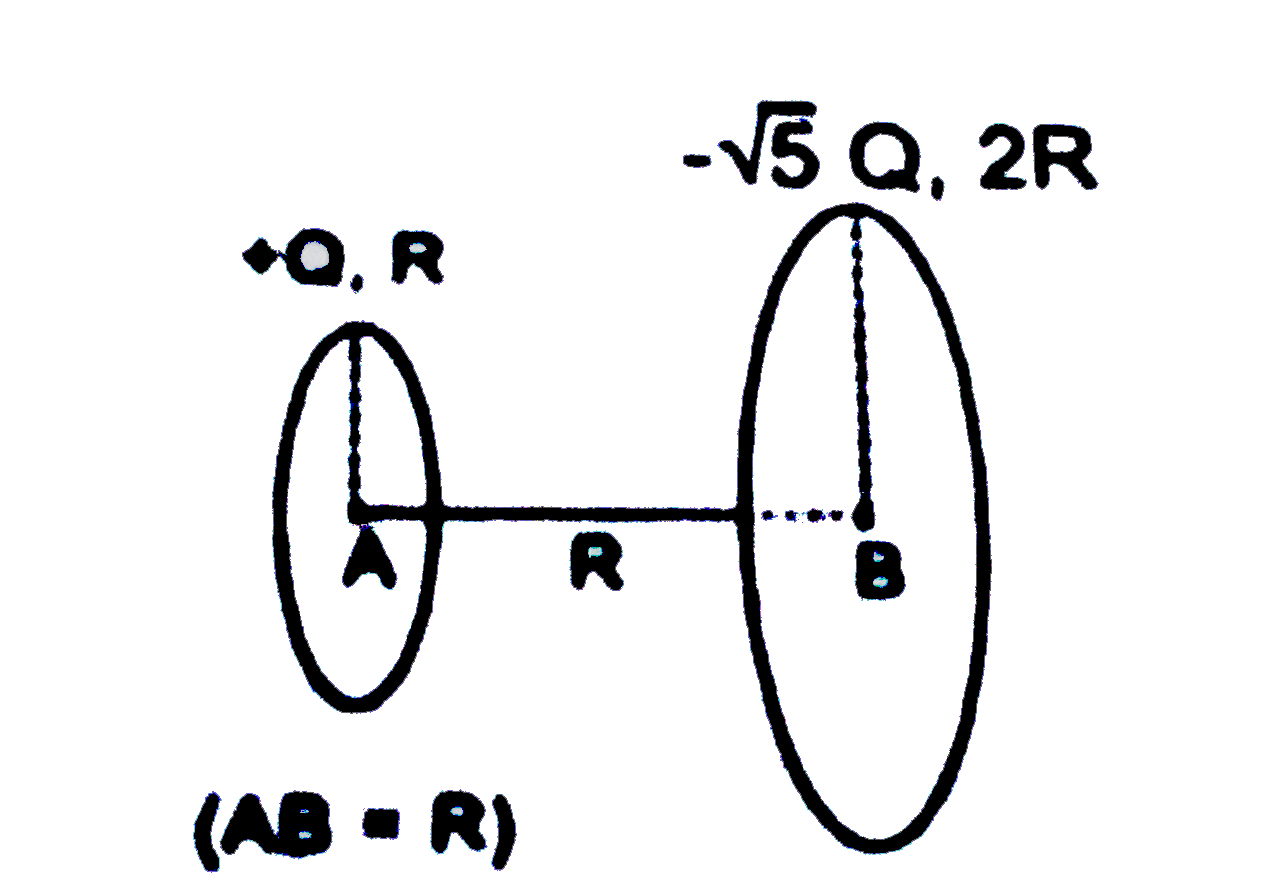 View Solution
View SolutionThe mass of an electron is m, charge is e and it is accelerated form rest through a potential difference of V volts. The velocity acquired by electron will be :
View Solution
