A coil carrying electric current is placed in uniform magnetic field
torque is formed
emf is induced
Both (a) and (b) are correct
None of the above
The correct Answer is:a
To solve the problem of whether a coil carrying electric current placed in a uniform magnetic field experiences torque, EMF, or both, we can follow these steps:
1. Understanding the Setup:
We have a coil that carries an electric current and is placed in a uniform magnetic field. We need to analyze the forces acting on the coil and determine if torque or EMF is induced.
Hint: Visualize the coil and the magnetic field direction. Draw a diagram to help you understand the orientation.
2. Identify the Forces on the Coil:
The force on a current-carrying conductor in a magnetic field is given by the equation:
F=I⋅L×B
where I is the current, L is the length of the conductor, and B is the magnetic field.
Hint: Remember that the direction of the force can be determined using the right-hand rule.
3. Analyze Each Segment of the Coil:
For segments of the coil parallel to the magnetic field (let's say segments P and Q), the angle θ between the current direction and magnetic field is 0 or 180 degrees. Therefore, the force on these segments will be zero:
F=0(for segments P and Q)
Hint: Check the angles between the current direction and the magnetic field for each segment.
4. Calculate Forces on Other Segments:
For the segments perpendicular to the magnetic field (let's say segments R and S), the angle θ is 90 degrees, resulting in maximum force:
F=I⋅L⋅B(for segments R and S)
The forces will act in opposite directions on these segments.
Hint: Use the right-hand rule to find the direction of the forces on these segments.
5. Determine the Torque:
The forces acting on segments R and S will create a torque about the axis of the coil. The torque τ can be calculated as:
τ=r⋅F
where r is the distance from the axis to the line of action of the force.
Hint: Visualize how the forces will cause the coil to rotate about its axis.
6. Check for Induced EMF:
The induced EMF in a coil can be calculated using:
EMF=−dΦdt
where Φ is the magnetic flux. In this case, since the area of the coil and the magnetic field are uniform and constant, there is no change in flux:
EMF=0
Hint: Consider whether the area or magnetic field is changing over time.
7. Conclusion:
Since torque is present due to the forces on segments R and S, but no EMF is induced, the correct conclusion is that torque is formed, but EMF is not induced.
Final Answer: Torque is formed (Option A), and EMF is not induced.
We have a coil that carries an electric current and is placed in a uniform magnetic field. We need to analyze the forces acting on the coil and determine if torque or EMF is induced.
The force on a current-carrying conductor in a magnetic field is given by the equation:
F=I⋅L×B
where I is the current, L is the length of the conductor, and B is the magnetic field.
For segments of the coil parallel to the magnetic field (let's say segments P and Q), the angle θ between the current direction and magnetic field is 0 or 180 degrees. Therefore, the force on these segments will be zero:
F=0(for segments P and Q)
For the segments perpendicular to the magnetic field (let's say segments R and S), the angle θ is 90 degrees, resulting in maximum force:
F=I⋅L⋅B(for segments R and S)
The forces will act in opposite directions on these segments.
The forces acting on segments R and S will create a torque about the axis of the coil. The torque τ can be calculated as:
τ=r⋅F
where r is the distance from the axis to the line of action of the force.
The induced EMF in a coil can be calculated using:
EMF=−dΦdt
where Φ is the magnetic flux. In this case, since the area of the coil and the magnetic field are uniform and constant, there is no change in flux:
EMF=0
Since torque is present due to the forces on segments R and S, but no EMF is induced, the correct conclusion is that torque is formed, but EMF is not induced.
Similar Questions
A coil carrying electric current is placed in uniform magnetic field
View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to

View SolutionWhat is the force experienced by a semicircular wire of radius R when it is carrying a current l and is placed in a uniform magnetic field of induction B as shown in figure. ?
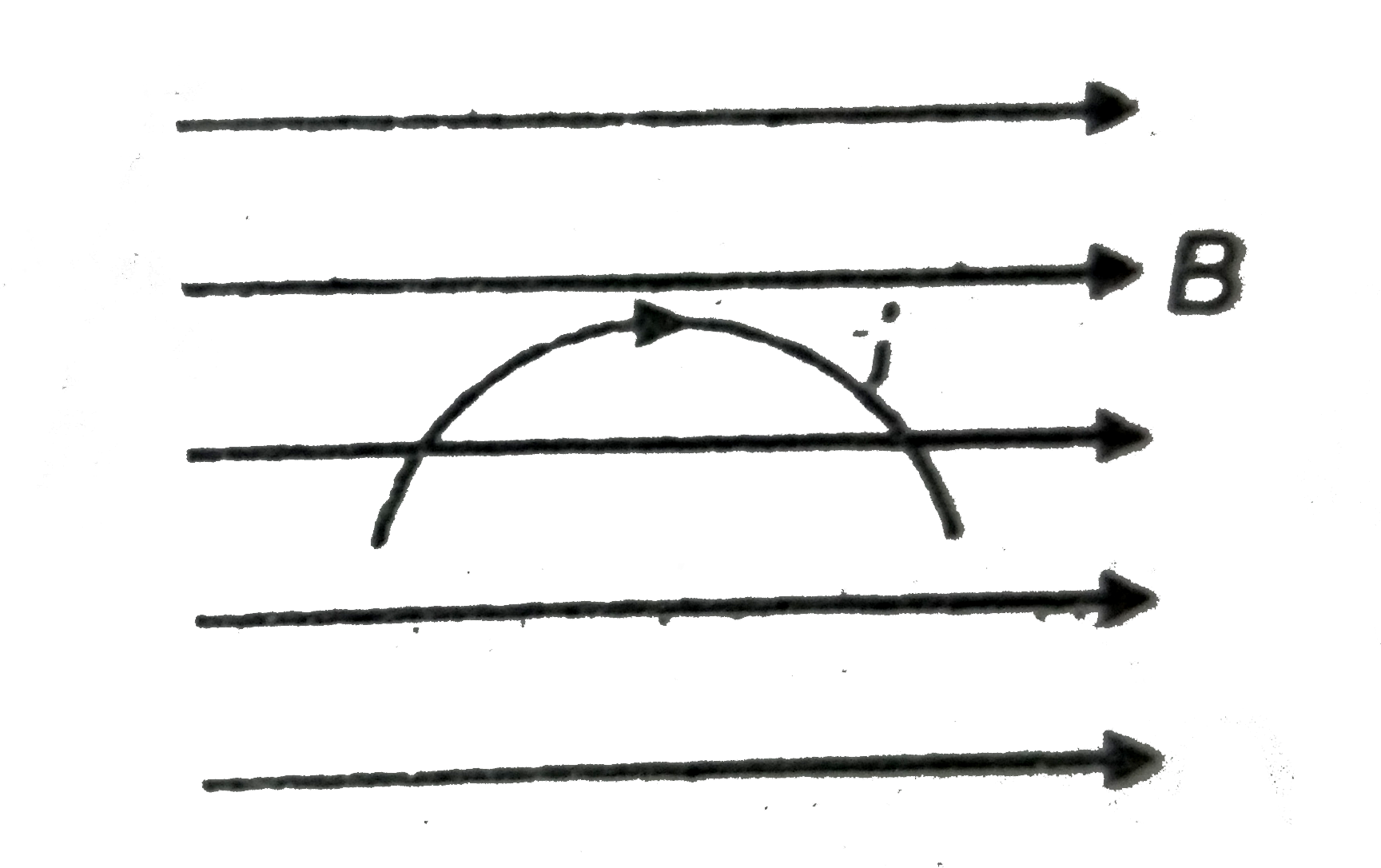
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionA loop of Irregular shape made of flexible conducting wire carrying clockwise current is placed in uniform inward magnetic field, such that its plane is perpendicular to the field. Then the loop
View SolutionA circular coil carrying current I is placed in a region of uniform magnetic field acting perpendicular to a coil as shown in te Mark correct option
 .
.
View SolutionStatement 1: The net force on a closed circular current carrying loop placed in a uniform magnetic field is zero.
Statement 2: The torque produced in a conducting circular ring is zero when it is placed in a uniform magnetic field such that the magnetic field is perpendicular to the plane of loop.
View SolutionA current carrying conducting square frame of side I carrying current I is placed in a uniform transverse magnetic field →B as shown in the figure. Choose the incorrect statement.
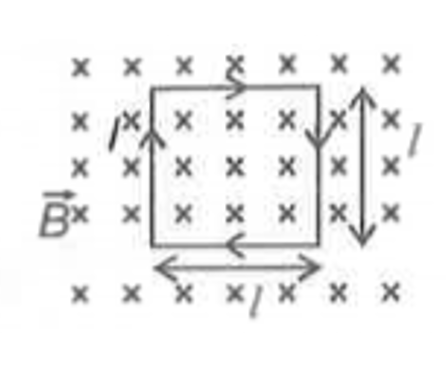
View SolutionA circular coil of 20turns and radius 10cm carries a current of 5A. It is placed in a uniform magnetic field of 0⋅10T. Find the torque acting on the coil when the magnetic field is applied (a) normal to the plane of the coil (b) in the plane of coil. Also find out the total force acting on the coil.
View SolutionA rectangular coil 20cm×20cm has 100 turns and carries a current of 1A. It is placed in a uniform magnetic field B=0.5T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View Solution
