A conducting circular loop is placed in a uniform magnetic field 0.04T with its plane perpendicular to the magnetic field. The radius of the loop starts shrinking at 2mm/sec . The induced emf in the loop when the radius is 2cm is:
(1.) 3.2
π
μ
V
(2.)
4.8
π
μ
V
(3.)
0.8
π
μ
V
(4.)
1.6
π
μ
V
3.2πμV
4.8πμV
0.8πμV
1.6πμV
The correct Answer is:a
To solve the problem, we need to find the induced electromotive force (emf) in a conducting circular loop placed in a uniform magnetic field as the radius of the loop shrinks. We will use Faraday's law of electromagnetic induction.
1. Identify the given values:
- Magnetic field strength, B=0.04T
- Radius of the loop when calculating, r=2cm=2×10−2m
- Rate of change of radius, drdt=−2mm/s=−2×10−3m/s (negative because the radius is shrinking)
2. Calculate the area of the loop:
- The area A of a circular loop is given by:
A=πr2
- Substituting the value of r:
A=π(2×10−2)2=π(4×10−4)=4π×10−4m2
3. Use Faraday's law to find the induced emf:
- The induced emf ε is given by:
ε=−BdAdt
- We can express dAdt in terms of r:
dAdt=ddt(πr2)=π⋅2rdrdt
- Substituting r=2×10−2m and drdt=−2×10−3m/s:
dAdt=π⋅2(2×10−2)⋅(−2×10−3)=−8π×10−5m2/s
4. Substituting into the emf formula:
- Now substitute B and dAdt into the emf equation:
ε=−BdAdt=−0.04⋅(−8π×10−5)=0.04⋅8π×10−5
- Calculating this gives:
ε=3.2×10−6πV
5. Convert to microvolts:
- Since 10−6 is equivalent to micro, we can express the final answer as:
ε=3.2πμV
Final Answer:
The induced emf in the loop when the radius is 2cm is:
ε=3.2πμV
- Magnetic field strength, B=0.04T
- Radius of the loop when calculating, r=2cm=2×10−2m
- Rate of change of radius, drdt=−2mm/s=−2×10−3m/s (negative because the radius is shrinking)
- The area A of a circular loop is given by:
A=πr2
- Substituting the value of r:
A=π(2×10−2)2=π(4×10−4)=4π×10−4m2
- The induced emf ε is given by:
ε=−BdAdt
- We can express dAdt in terms of r:
dAdt=ddt(πr2)=π⋅2rdrdt
- Substituting r=2×10−2m and drdt=−2×10−3m/s:
dAdt=π⋅2(2×10−2)⋅(−2×10−3)=−8π×10−5m2/s
- Now substitute B and dAdt into the emf equation:
ε=−BdAdt=−0.04⋅(−8π×10−5)=0.04⋅8π×10−5
- Calculating this gives:
ε=3.2×10−6πV
- Since 10−6 is equivalent to micro, we can express the final answer as:
ε=3.2πμV
The induced emf in the loop when the radius is 2cm is:
ε=3.2πμV
Similar Questions
A conducting circular loop is in a perpendicular magnetic field of induction 10−2T If the radius of the loop starts shrinking at a uniform rate of 1 mm/s, then the e.m.f. induced in the loop at the instant when its radius is 10 cm will be
View SolutionA conducting circular loop is placed in a uniform magnetic field, B=0.025T with its plane perpendicular to the loop. The radius of the loop is made to shrink at a constant rate of 1 mms^(-1) . The induced emf when the radius is 2 cm is
View SolutionA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
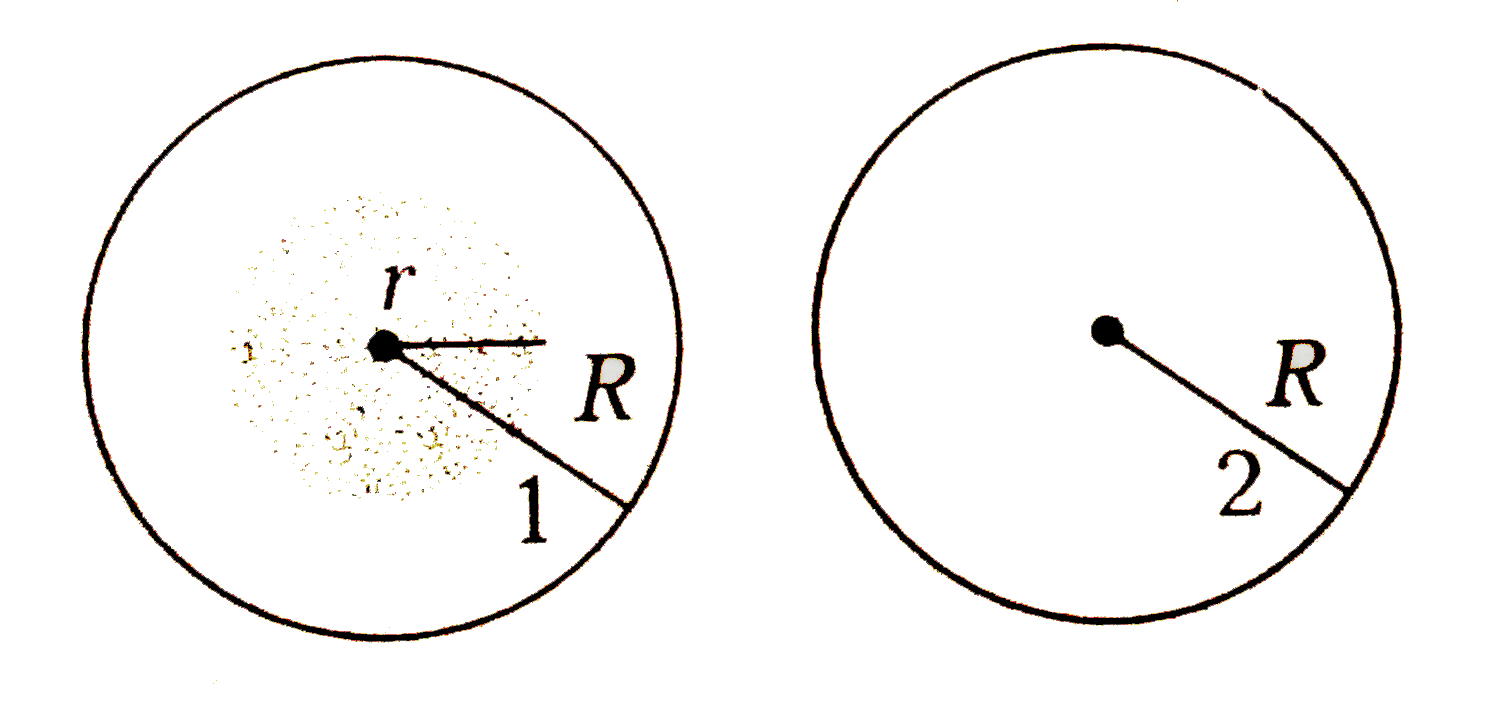
Zero in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and − d B d t π 2 in loop 2
− d B d t π R 2 in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and zero in loop 2
View SolutionA conducting circualr loop is placed in a unifrom magentic field , B= 0.025 T with its plane perpendicular to the loop .The radius of the loop is made to shrink at a constant rate of 1 mms−1 .The induced emf when the radius is 2cm ,is
View Solutionएक वृत्ताकार चालक पाश को एकसमान चुंबकीय क्षेत्र 0.04 T में इस प्रकार रखा जाता है कि इसका तल चुम्बकीय क्षेत्र के लंबवत होता है। पाश की त्रिज्या 2 mm s−1 पर सिकुड़ना प्रारंभ करती है। जब त्रिज्या 2 cm है तब पाश में प्रेरित विद्युत वाहक बल कितना है?
View Solutionएक चालक वृत्तीय फंद को 0.04T के अचर चुंबकीय क्षेत्र में इस तरह रखा है कि फंद का तल चुंबकीय क्षेत्र की दिशा से लम्ब दिशा में है। फंद की त्रिज्या 2mm/s की दर से घटने लगती है। जब फंद की त्रिज्या 2cm होगी तो इसमें प्रेरित वि० वा० ब० (emf) का मान होगा
View SolutionA conductlng circular loop is placed in a uniform magnetic field 0.04 T with its plane perpendicular to the magnetic field. The radius of the loop starts shrinking at 2 mm//s . The induced emf in the loop when the radius is 2 cm is:
View Solution
