In an circuit, the rms value of the current is related to the peak current as
1)
2)
3)
4)
The correct Answer is:D
To find the relationship between the RMS value of the current Irms and the peak current I0 in an AC circuit, we can follow these steps:
1. Understanding RMS Current:
The RMS (Root Mean Square) value of the current is defined as the value of the direct current (DC) that would deliver the same power to a resistor as the alternating current (AC) does over one complete cycle.
2. Power Equivalence:
The power consumed by the AC circuit can be expressed as:
P=I2rmsR
where R is the resistance.
3. Expression for AC Current:
The instantaneous current in an AC circuit can be expressed as:
I(t)=I0sin(ωt)
where I0 is the peak current and ω is the angular frequency.
4. Calculating Power in AC Circuit:
The average power over one complete cycle can also be expressed as:
P=1T∫T0I(t)2Rdt
where T is the time period of the AC signal.
5. Substituting for I(t):
Substitute I(t) into the power equation:
P=1T∫T0(I0sin(ωt))2Rdt
Simplifying gives:
P=RI201T∫T0sin2(ωt)dt
6. Using Trigonometric Identity:
We can use the identity sin2(x)=1−cos(2x)2 to simplify the integral:
∫T0sin2(ωt)dt=T2
Thus, the average power becomes:
P=RI201T⋅T2=RI202
7. Equating Powers:
Now, equate the two expressions for power:
I2rmsR=RI202
Cancel R from both sides (assuming R≠0):
I2rms=I202
8. Taking the Square Root:
Finally, taking the square root of both sides gives:
Irms=I0√2
Final Answer:
The relationship between the RMS value of the current Irms and the peak current I0 is:
Irms=I0√2
The RMS (Root Mean Square) value of the current is defined as the value of the direct current (DC) that would deliver the same power to a resistor as the alternating current (AC) does over one complete cycle.
The power consumed by the AC circuit can be expressed as:
P=I2rmsR
where R is the resistance.
The instantaneous current in an AC circuit can be expressed as:
I(t)=I0sin(ωt)
where I0 is the peak current and ω is the angular frequency.
The average power over one complete cycle can also be expressed as:
P=1T∫T0I(t)2Rdt
where T is the time period of the AC signal.
Substitute I(t) into the power equation:
P=1T∫T0(I0sin(ωt))2Rdt
Simplifying gives:
P=RI201T∫T0sin2(ωt)dt
We can use the identity sin2(x)=1−cos(2x)2 to simplify the integral:
∫T0sin2(ωt)dt=T2
Thus, the average power becomes:
P=RI201T⋅T2=RI202
Now, equate the two expressions for power:
I2rmsR=RI202
Cancel R from both sides (assuming R≠0):
I2rms=I202
Finally, taking the square root of both sides gives:
Irms=I0√2
The relationship between the RMS value of the current Irms and the peak current I0 is:
Irms=I0√2
Similar Questions
Knowledge Check
The rms value of current in an ac circuit is 25 A, then peak current is
A35.36mAB35.36AC3.536AD49.38AIn the circuit shown, the value of currents I1,I2andI3 are
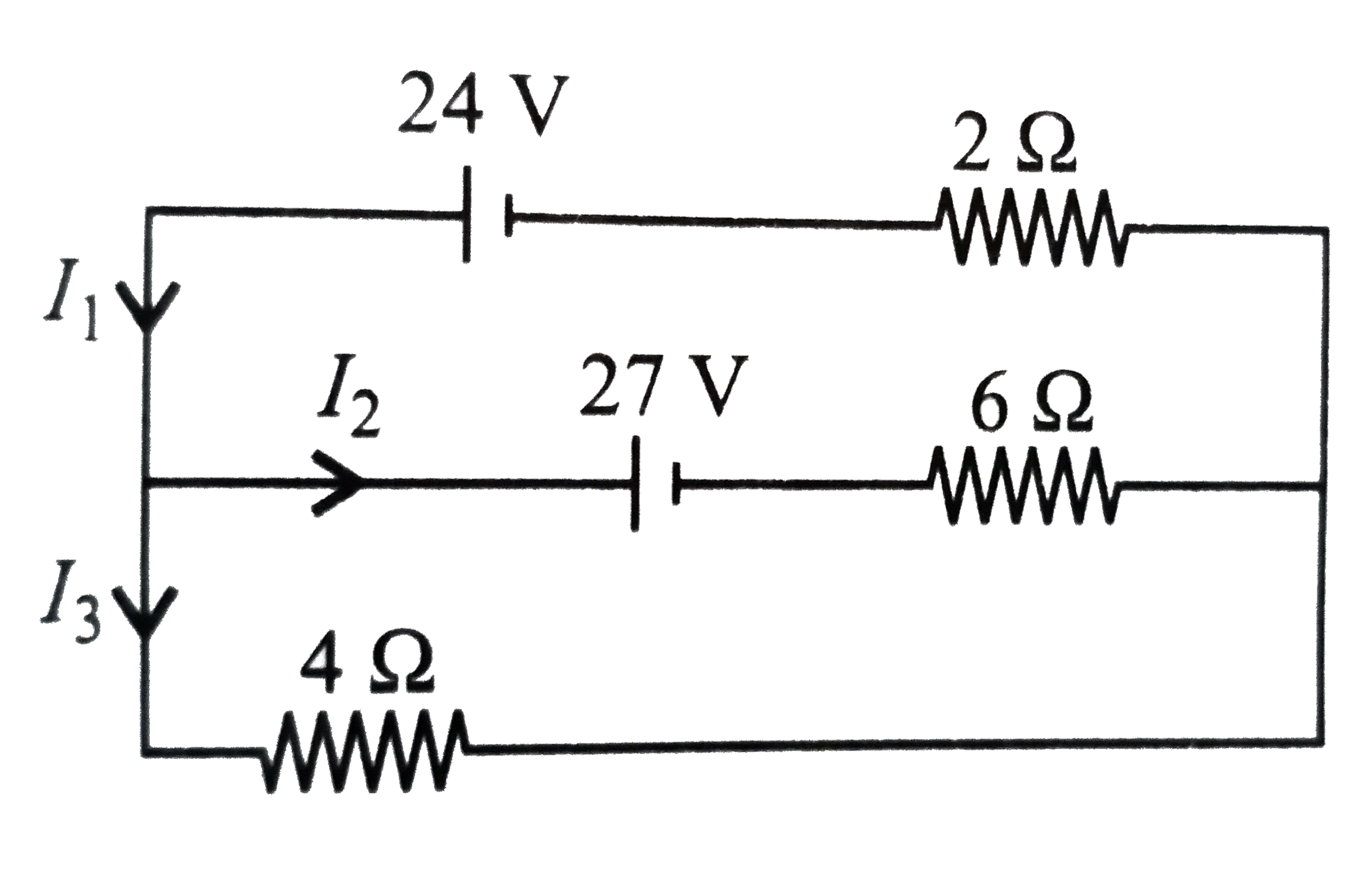 A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92A
A3A,−3A2A,92AB92A,−32AC5A,4A,−3AD7A,54A,92AIf the rms current in a 50 Hz ac circuit is 5 A, the value of the current 1/300 second after its value becomes zero is
A5√2AB5√32AC56AD5√2A
If i=t2,0<t<T then r.m.s. value of current is
View SolutionStatement 1: In the purely resistive element of a series LCR, ac circuit the maximum value of rms current increase with increase in the angular frequency of the applied emf.
Statement 2: Imax=εmaxZ,Z= ⎷R2+(ωL−1(ωC)2),
where (Imax) is the peak current in a cycle.
View SolutionIf the rms current in a 50 Hz ac circuit is 5 A, the value of the current 1/300 second after its value becomes zero is
View SolutionIf the rms current in a 50 Hz ac circuit is 5 A, the value of the current 1/300 second after its value becomes zero is
View SolutionThe value of current I in the circuit will be
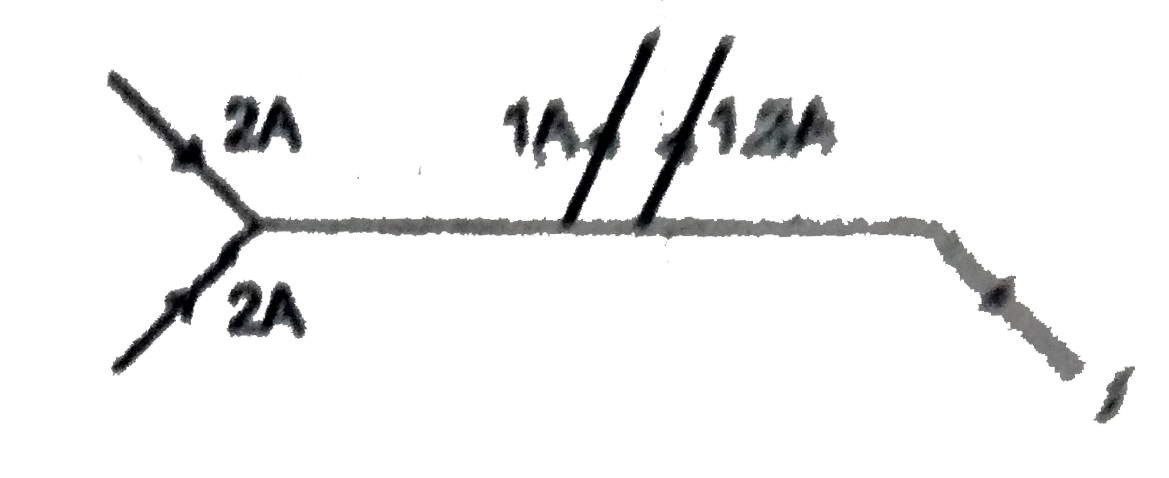
View Solution
