An object of mass 3kg is at rest. Now a force of →F=6t2ˆI+4tˆj is applied on the object, the velocity of object at t=3s is.
18ˆi+3ˆj
18ˆi+6ˆj
3ˆi+18ˆj
19ˆi+4ˆj
The correct Answer is:B
To find the velocity of the object at t=3 seconds, we can follow these steps:
Step 1: Identify the given values
- Mass of the object, m=3kg
- Force applied, →F=6t2^i+4t^j
- Time, t=3s
Step 2: Calculate acceleration
Using Newton's second law, the acceleration →a can be calculated using the formula:
→a=→Fm
Substituting the values:
→a=6t2^i+4t^j3
This simplifies to:
→a=2t2^i+43t^j
Step 3: Relate acceleration to velocity
Acceleration can also be expressed as:
→a=d→vdt
Thus, we can write:
d→v=→adt
Substituting for →a:
d→v=(2t2^i+43t^j)dt
Step 4: Integrate to find velocity
Integrating both sides from t=0 to t=3 seconds:
∫V0d→v=∫30(2t2^i+43t^j)dt
This gives:
→v=(23t3^i+46t2^j)30
Step 5: Evaluate the integral
Calculating the limits:
→v=(23(33)^i+46(32)^j)−(23(03)^i+46(02)^j)
This simplifies to:
→v=(23(27)^i+46(9)^j)
→v=18^i+6^j
Final Result
Thus, the velocity of the object at t=3s is:
→v=18^i+6^j
- Mass of the object, m=3kg
- Force applied, →F=6t2^i+4t^j
- Time, t=3s
Using Newton's second law, the acceleration →a can be calculated using the formula:
→a=→Fm
Substituting the values:
→a=6t2^i+4t^j3
This simplifies to:
→a=2t2^i+43t^j
Acceleration can also be expressed as:
→a=d→vdt
Thus, we can write:
d→v=→adt
Substituting for →a:
d→v=(2t2^i+43t^j)dt
Integrating both sides from t=0 to t=3 seconds:
∫V0d→v=∫30(2t2^i+43t^j)dt
This gives:
→v=(23t3^i+46t2^j)30
Calculating the limits:
→v=(23(33)^i+46(32)^j)−(23(03)^i+46(02)^j)
This simplifies to:
→v=(23(27)^i+46(9)^j)
→v=18^i+6^j
Thus, the velocity of the object at t=3s is:
→v=18^i+6^j
Similar Questions
An object of mass 3 kg is at rest . Now a force F=6t2ˆi+2tˆj is applied on the object . Find the velocity of the object at t =3 sec.
View SolutionAn object of mass 2 kg at rest at origin starts moving under the action of a force
→F=(3t2ˆi+4tˆj)N The velocity of the object at t = 2 s will be -
View Solution
Knowledge Check
A body with mass 5 kg is acted upon by a force →F=(−3ˆi+4ˆj)N. If its initial velocity at t =0 is →v=6ˆi−12ˆjms−1, the time at which it will just have a velocity along the y-axis is :
A0B10sC2sD15s
A body with mass 5 kg is acted upon by a force →F=(−3ˆi+4ˆj)N. If its initial velocity at t =0 is →v=(6ˆi−12ˆj)ms−1, the time at which it will just have a velocity along the y-axis is :
View SolutionA body with mass 5 kg is acted upon by a force →F=(−3ˆi+4ˆj)N. If its initial velocity at t =0 is →v=6ˆi−12ˆjms−1, the time at which it will just have a velocity along the y-axis is :
View SolutionA body of mass 1kg begins to move under the action of a time dependent force →F=(2tˆi+3t2ˆj)N, where ˆi and ˆj are unit vectors along x-and y-axes. What power will be developed by the force at the time t ?
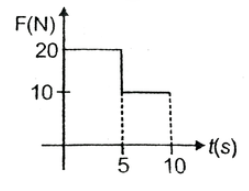
View SolutionForce is applied on an object of mass 2 kg at rest on a frictionless horizontal surface as shown in the graph. The speed of object at t=10 s will be
View SolutionThe displacement s of an object is given as a function of time t by the following equation s=2t+5t2+3t3. Calculate the instantaneous velocity of the object at t = 1 s.
View SolutionThe displacement x of an object is given as a function of time x=2t+3t2
Calculate the instantaneous velocity of the object at t = 2 s
View SolutionThe displacement x of an object is given as a funstion of time, x=2t+3t2. The instantaneous velocity of the object at t = 2 s is
View Solution
