The speed of a wave in a medium is 760 m/s. If 3600 waves are passing through a point in the medium in 2 min, then their wavelength is
13.8 m
25.3 m
41.5 m
57.2 m
The correct Answer is:b
To solve the problem step by step, we will follow these calculations:
Step 1: Convert time from minutes to seconds
Given that the time is 2 minutes, we need to convert this into seconds for our calculations.
t=2 minutes=2×60=120 seconds
Hint: Remember that 1 minute is equal to 60 seconds.
Step 2: Calculate the frequency of the waves
We know that frequency (n) is the number of waves passing through a point in a given time. Here, 3600 waves pass in 120 seconds.
n=Number of wavesTime in seconds=3600120=30 Hz
Hint: Frequency is calculated by dividing the total number of waves by the total time taken.
Step 3: Use the wave speed formula
The relationship between wave speed (V), frequency (n), and wavelength (λ) is given by the equation:
V=nλ
We can rearrange this to find the wavelength:
λ=Vn
Hint: This formula shows how speed, frequency, and wavelength are interconnected.
Step 4: Substitute the values into the wavelength formula
We know the speed of the wave (V) is 760 m/s and the frequency (n) we calculated is 30 Hz. Now we can find the wavelength (λ):
λ=760 m/s30 Hz=76030≈25.33 m
Hint: When substituting values, ensure that the units are consistent (meters per second for speed and Hertz for frequency).
Step 5: Round the answer
The wavelength can be rounded to two decimal places:
λ≈25.33 m
Hint: Rounding is often necessary for clarity, especially in physical measurements.
Final Answer
The wavelength of the wave is approximately 25.33 meters.
Given that the time is 2 minutes, we need to convert this into seconds for our calculations.
t=2 minutes=2×60=120 seconds
We know that frequency (n) is the number of waves passing through a point in a given time. Here, 3600 waves pass in 120 seconds.
n=Number of wavesTime in seconds=3600120=30 Hz
The relationship between wave speed (V), frequency (n), and wavelength (λ) is given by the equation:
V=nλ
We can rearrange this to find the wavelength:
λ=Vn
We know the speed of the wave (V) is 760 m/s and the frequency (n) we calculated is 30 Hz. Now we can find the wavelength (λ):
λ=760 m/s30 Hz=76030≈25.33 m
The wavelength can be rounded to two decimal places:
λ≈25.33 m
The wavelength of the wave is approximately 25.33 meters.
Similar Questions
Knowledge Check
In a transverse wave, the particles of the medium
Avibrate in a direction perpendicular to the direction of the propagation.Bvibrate in a direction parallel to the direction or of the propagationCmove in circleDmove in ellipseA sound wave travels with a velocity of 300 m s−1 through a gas. 9 beats are produced in 3 s when two waves pass through it simultaneously. lf one of the waves has 2 m wavelength, the wavelength of the other wave is a) 1.98 m b) 2.04 m c) 2.06 m d) 1.99 m
A1.98 mB2.04 mC2.06 mD1.99 m
The speed of wave in a certain medium is 100ms. If 1000 waves pass over a certain point of the medium in 1 minute 40 second, the wavelength is
View SolutionTransverse waves propagate in a medium with
View SolutionWhen a wave passes through a medium, what type of motion do the particles execute ?
View Solution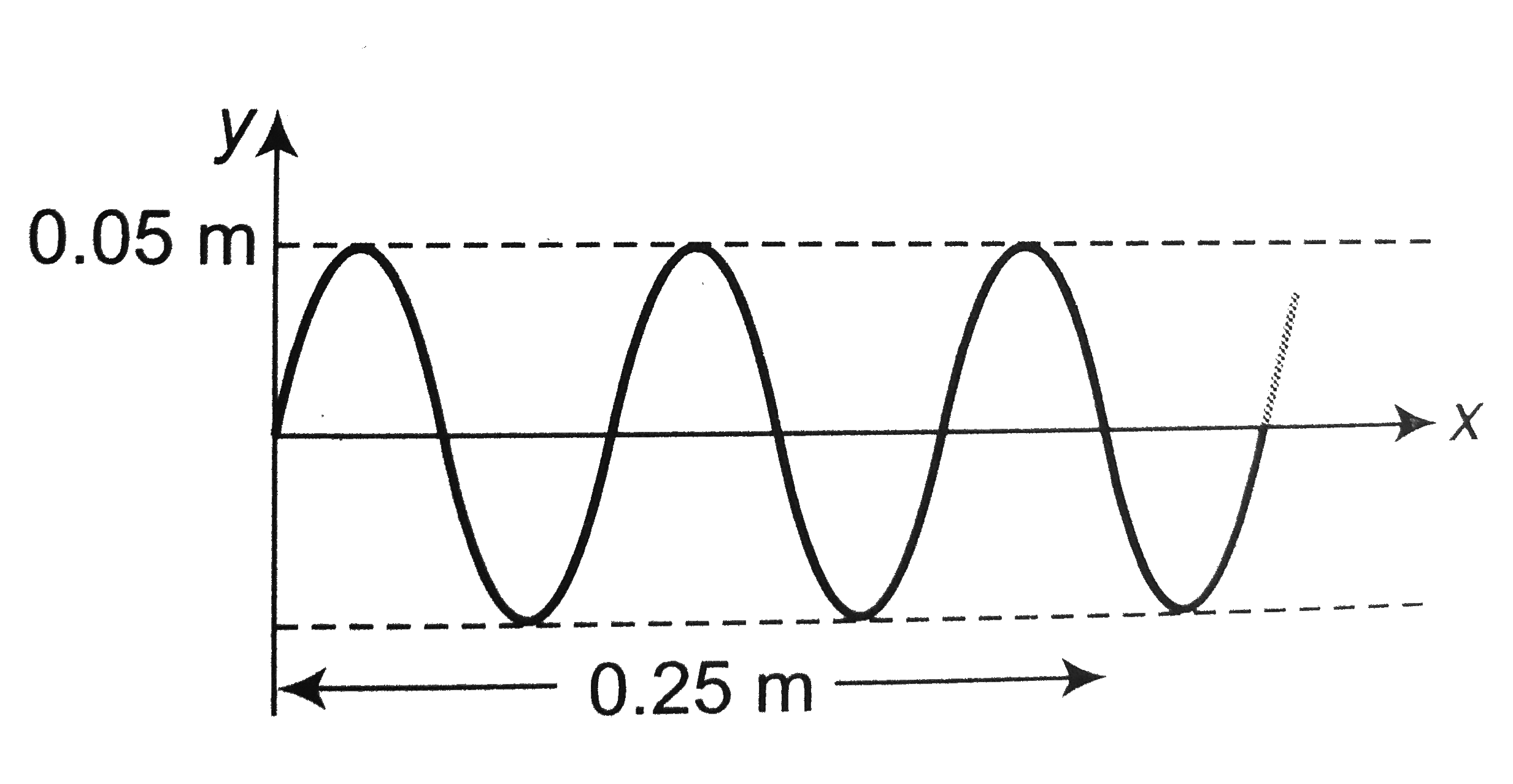
If the speed of the wave shown in the figure is 330m/s in the given medium then the equation of the wave propagating in the positive x-direction will be (all quantities are in M.K.S units)
View SolutionA : In a material medium the speed of a particle can be more than the speed of light in that medium.
R : In the phenomenon of green house effect, low wavelength radiation is allowed to pass but high wavelength radiation is not allowed to pass.
View SolutionIf a wave is going from one medium to another, then
View Solution
