Two thin lenses of focal length f1 and f2 are in contact and coaxial. The power of the combination is
√f1f2
√f2f1
f1+f22
f1f2f1f2
The correct Answer is:D
To find the power of the combination of two thin lenses in contact and coaxial, we can follow these steps:
Step 1: Understand the Concept of Power
The power P of a lens is defined as the reciprocal of its focal length f:
P=1f
where P is measured in diopters (D) and f is in meters.
Step 2: Determine the Power of Each Lens
For two lenses with focal lengths f1 and f2:
- The power of the first lens P1 is:
P1=1f1
- The power of the second lens P2 is:
P2=1f2
Step 3: Combine the Powers
When two lenses are in contact and coaxial, the total power P of the combination is the sum of the individual powers:
P=P1+P2
Substituting the expressions for P1 and P2:
P=1f1+1f2
Step 4: Simplify the Expression
To combine the fractions, we can find a common denominator:
P=f2+f1f1f2
Step 5: Final Result
Thus, the power of the combination of the two lenses is:
P=f1+f2f1f2
The power P of a lens is defined as the reciprocal of its focal length f:
P=1f
where P is measured in diopters (D) and f is in meters.
For two lenses with focal lengths f1 and f2:
- The power of the first lens P1 is:
P1=1f1
- The power of the second lens P2 is:
P2=1f2
When two lenses are in contact and coaxial, the total power P of the combination is the sum of the individual powers:
P=P1+P2
Substituting the expressions for P1 and P2:
P=1f1+1f2
To combine the fractions, we can find a common denominator:
P=f2+f1f1f2
Thus, the power of the combination of the two lenses is:
P=f1+f2f1f2
Similar Questions
Two thin lenses of focal lengths f1 and f2 are in contact. The focal length of this combination is
View SolutionTwo thin lenses of focal lengths 20 cm and 25 cm are placed in a contact. The effective power of the combination is
View SolutionTwo thin lenses of focal lengths 20 cm and 25 cm are placed in a contact. The effective power of the combination is
View SolutionTwo thin lenses of focal lengths 20 cm and -20 cm are placed in contact with other. The combination has a focal length equal to
View Solution(a) Using the ray diagram for a system of two lenses of focal lengths f1andf2 in contact with each other, show that the two lens system can be regarded as equivalent to a single lens of focal length f, where
1f=1f1+1f2
Also write the relation for the equivalent power of the lens combination.
(b) Determine the position of the image formed by the lens combination given in the figure.
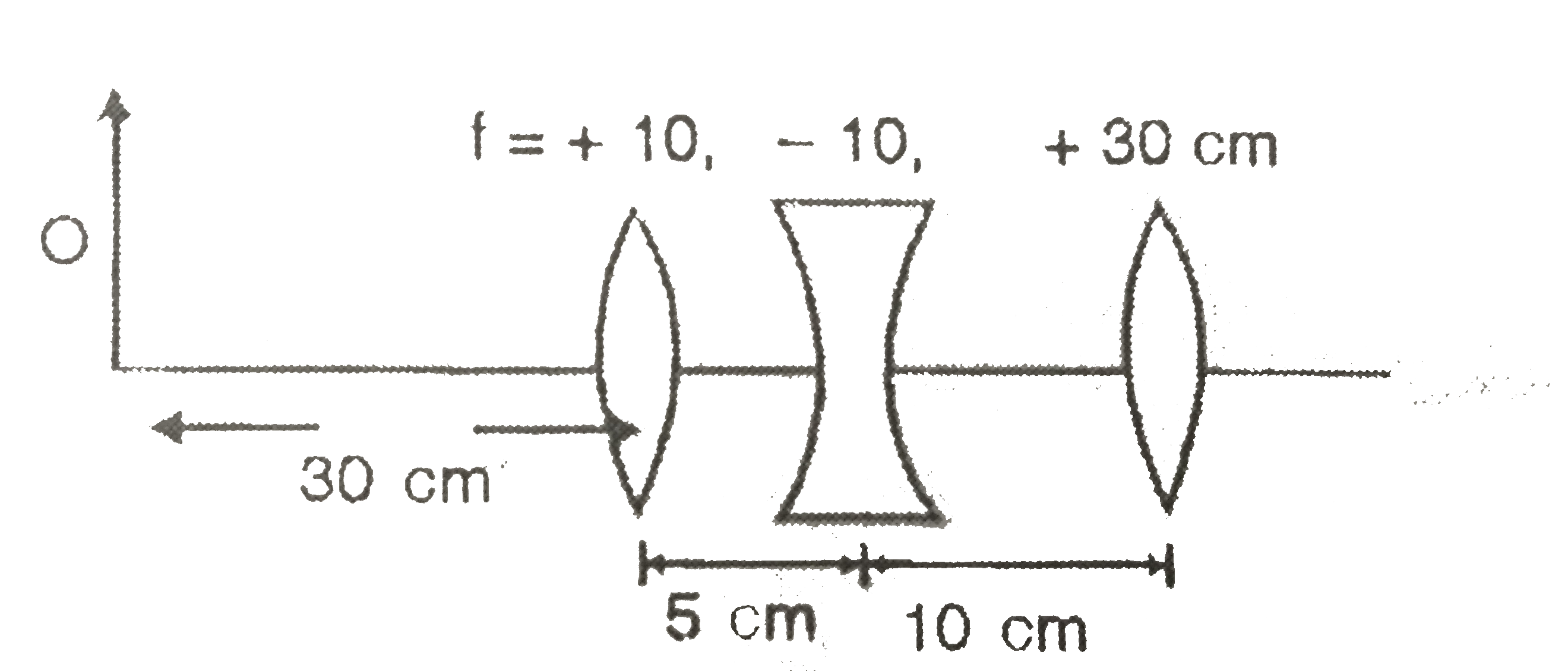
View SolutionTwo lenses of power −15D and +5D are in contact with each other. The focal length of the combination is
View SolutionTwo thin lenses of power +6Dand−2D are in contact. What is the focal length of the combination ?
View SolutionTwo thin lenses of power +5 D and -2.5 D are in contact. What is the focal length of the combination ?
View SolutionA convex lens of focal length A and a concave lens of focal length B are placed in contact. The focal length of the combination is
View SolutionWhen two thin lenses of focal lengths fi and f, are kept coaxially and in contact, prove that their cobined focal length "f" is given by :
1f=1f1+1f2
View Solution
