A lens if placed between a source of light and a wall. It forms images of areaA1 and A2 on the wall for its two different positions. The area of the source or light is
√A1A2
A1+A22
A1−A22
1A1+1A2
The correct Answer is:A
To solve the problem, we need to find the area of the source of light (denoted as AB) based on the areas of the images formed on the wall (A1 and A2) when the lens is in two different positions. Here’s a step-by-step solution:
Step 1: Understand the relationship between the areas and magnifications
When a lens forms an image of an object, the area of the image (A) is related to the area of the object (AB) and the magnification (M) by the formula:
A=M2×AB
This means that the area of the image is proportional to the square of the magnification times the area of the object.
Step 2: Set up equations for the two positions
For the first position of the lens, let the magnification be M1. The area of the image formed is:
A1=M21×AB
For the second position of the lens, let the magnification be M2. The area of the image formed is:
A2=M22×AB
Step 3: Rearrange the equations to express AB
From the first equation, we can express AB:
AB=A1M21
From the second equation, we can also express AB:
AB=A2M22
Step 4: Multiply the two equations
Now, if we multiply the two equations:
A1×A2=(M21×AB)×(M22×AB)
This simplifies to:
A1×A2=M21×M22×AB2
Step 5: Isolate AB2
Rearranging gives us:
AB2=A1×A2M21×M22
Step 6: Use the displacement method
According to the displacement method, when the lens is moved, the product of the magnifications for the two positions equals 1:
M1×M2=1
This implies:
M21×M22=1
Step 7: Substitute back into the equation
Substituting this back into our equation for AB2:
AB2=A1×A2
Taking the square root gives us:
AB=√A1×A2
Final Answer
Thus, the area of the source of light is:
AB=√A1×A2
When a lens forms an image of an object, the area of the image (A) is related to the area of the object (AB) and the magnification (M) by the formula:
A=M2×AB
This means that the area of the image is proportional to the square of the magnification times the area of the object.
For the first position of the lens, let the magnification be M1. The area of the image formed is:
A1=M21×AB
For the second position of the lens, let the magnification be M2. The area of the image formed is:
A2=M22×AB
From the first equation, we can express AB:
AB=A1M21
From the second equation, we can also express AB:
AB=A2M22
Now, if we multiply the two equations:
A1×A2=(M21×AB)×(M22×AB)
This simplifies to:
A1×A2=M21×M22×AB2
Rearranging gives us:
AB2=A1×A2M21×M22
According to the displacement method, when the lens is moved, the product of the magnifications for the two positions equals 1:
M1×M2=1
This implies:
M21×M22=1
Substituting this back into our equation for AB2:
AB2=A1×A2
Taking the square root gives us:
AB=√A1×A2
Thus, the area of the source of light is:
AB=√A1×A2
Similar Questions
A lens is placed between a source of light and screen. It forms real image on screen for two different positions. If height of one image is 20 cm and the other is 80 cm, then the height of source of light (in cm) is_____.
View SolutionA screen is placed a distance 40 cm away from an illuminated object. A converging lens is placed between the source and the screen and it is attempted to form the image of the source on the screen. If no position could be found, the focal length of the lens
View SolutionA bi-convex lens is placed between a light source and a concave mirror as shwon such that image of the light source coincides with itself. Then,
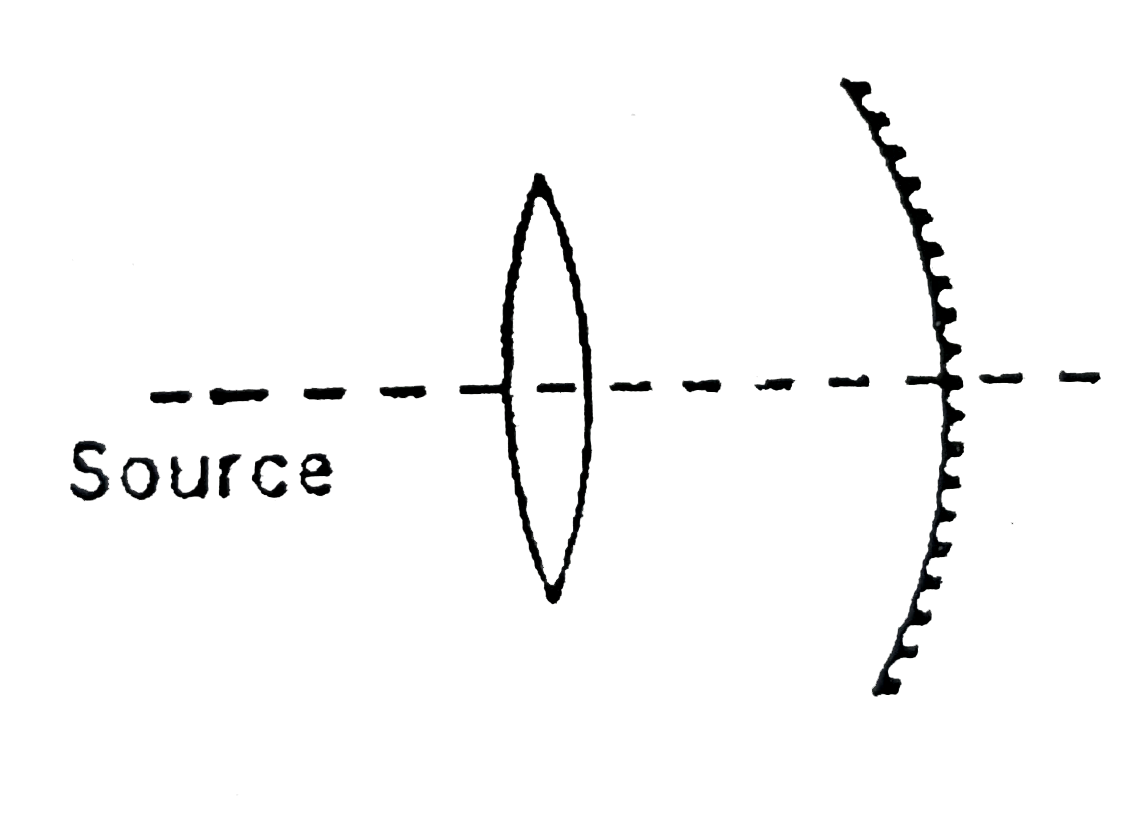
View Solutiona. Figure (a) shows the optical axis of a lens, the point source of light A, and its virtual image A′ . Trace the rays to find the position of the lens and of its focuses. What type of lens is it?

b. Solve the problem similar to the previous one using Figure.
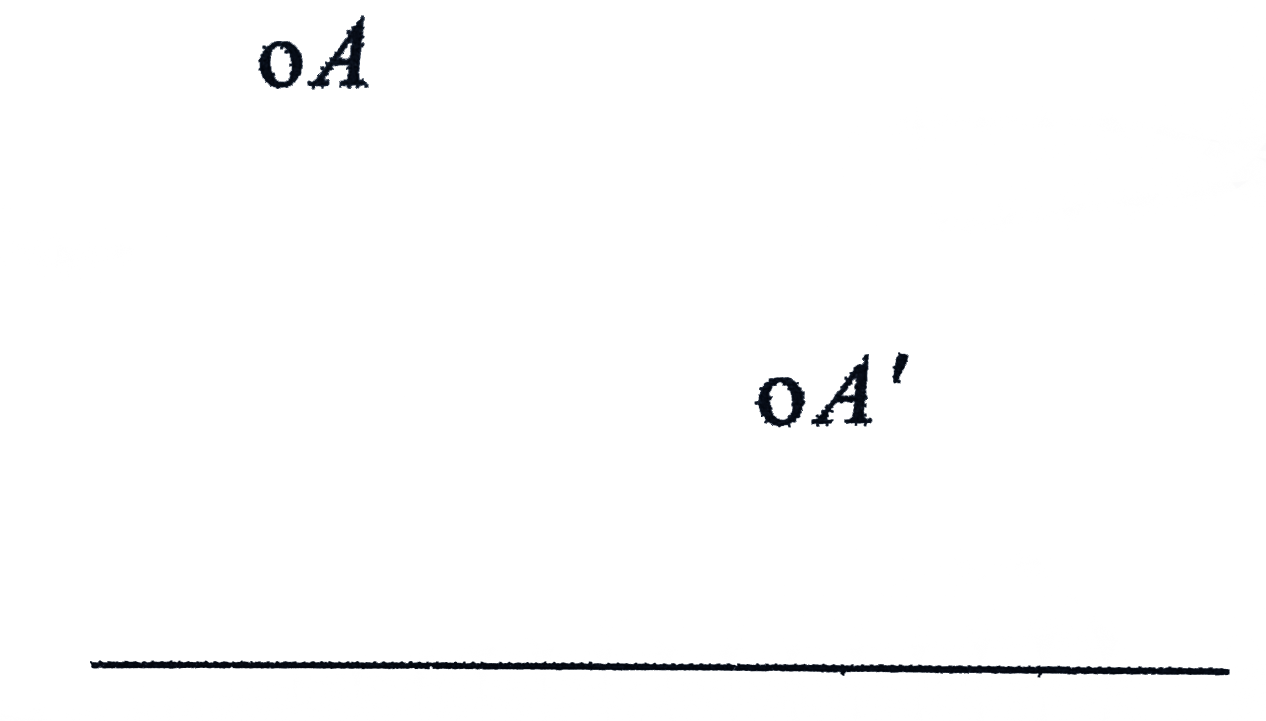
View Solutiona. Figure (a) shows the optical axis of a lens, the point source of light A, and its virtual image A′ . Trace the rays to find the position of the lens and of its focuses. What type of lens is it?

b. Solve the problem similar to the previous one using Figure.
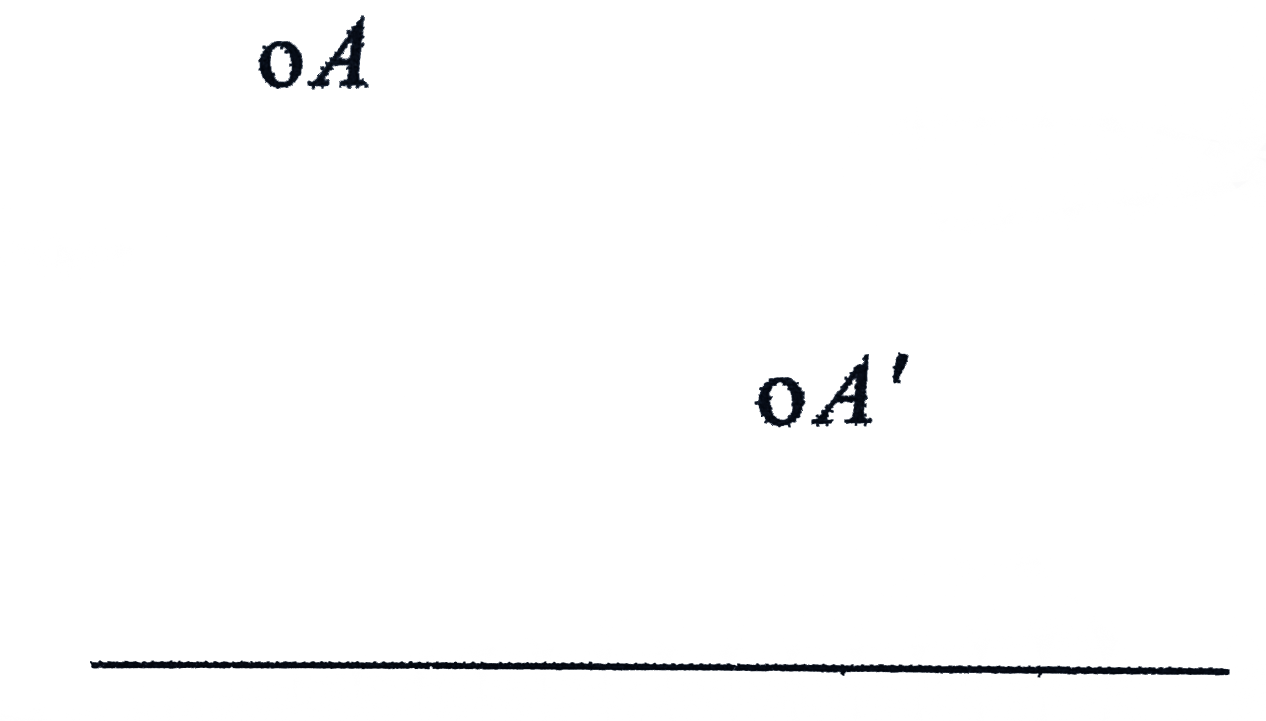
View SolutionThe internal surface of the walls of a sphere is specular. The radius of the sphere is R=36cm. A point source S is placed at a distance R/2 from the cneter of the sphere and sends light to the remote part of the sphere. Where will the image of the source be after two successive reflections from the remote and then nearest wall of the sphere? How will the position of the image change if the source sends light to the nearest wall first?Consider paraxial rays.
View SolutionSources 1 and 2 emit lights of different wavelengths whereas sources 3 and 4 emit light of different intensities.
The coherence
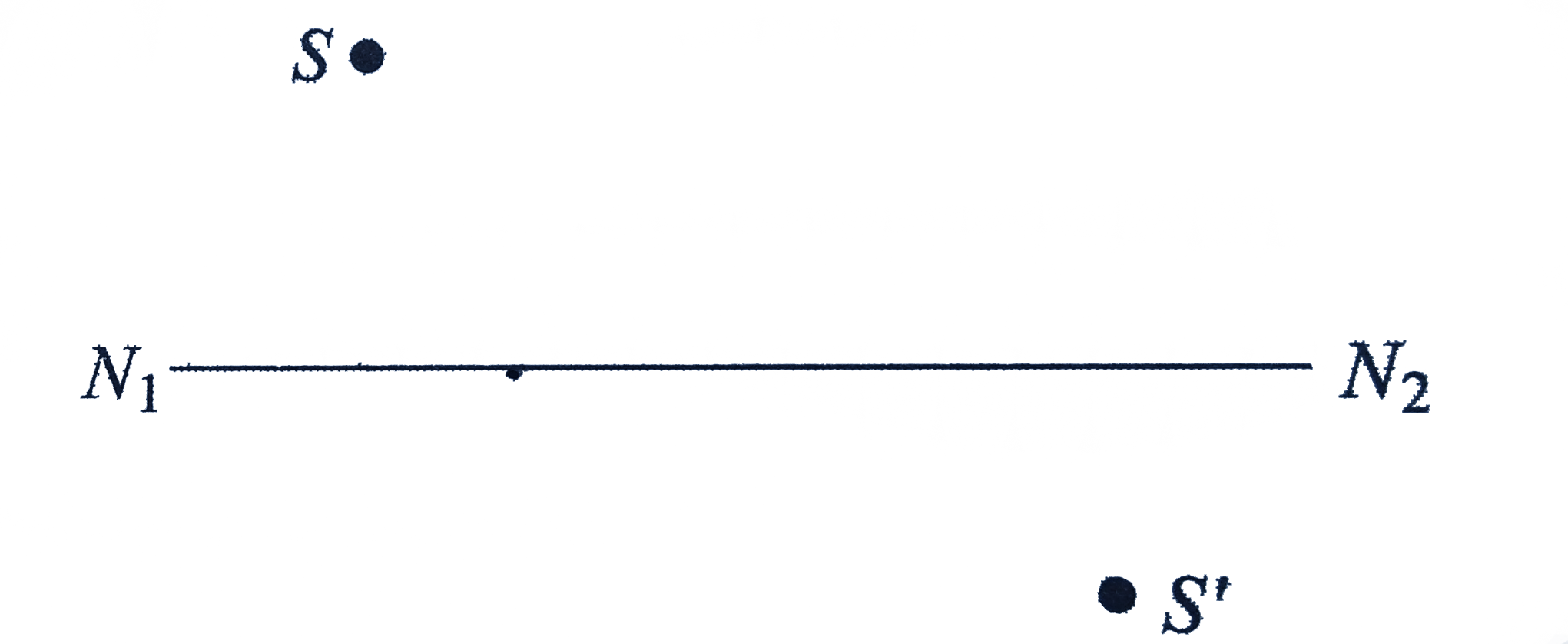
View SolutionPoint S′ is the image of a point source of light S in a spherical mirror whose optical axise is N1N2 (shown in Figure). Find by construction the position of the center of the mirror and its focus.
View SolutionA thin convex lens of refractive index μ=1.5 is placed between a point source of Light S and a screen A, shown in figure,. Light rays from the source S are brought to focus on the screen A, forming a point image P. The distance SP is equal to 50cm. Water (μ=4/3) is now poured into a vessel interposed between the object and the lens, and it is observed that when the water level is 8cm the screen has to be moved up by a distance of 6cm in order to get a sharp image. Find the focal length of the lens.
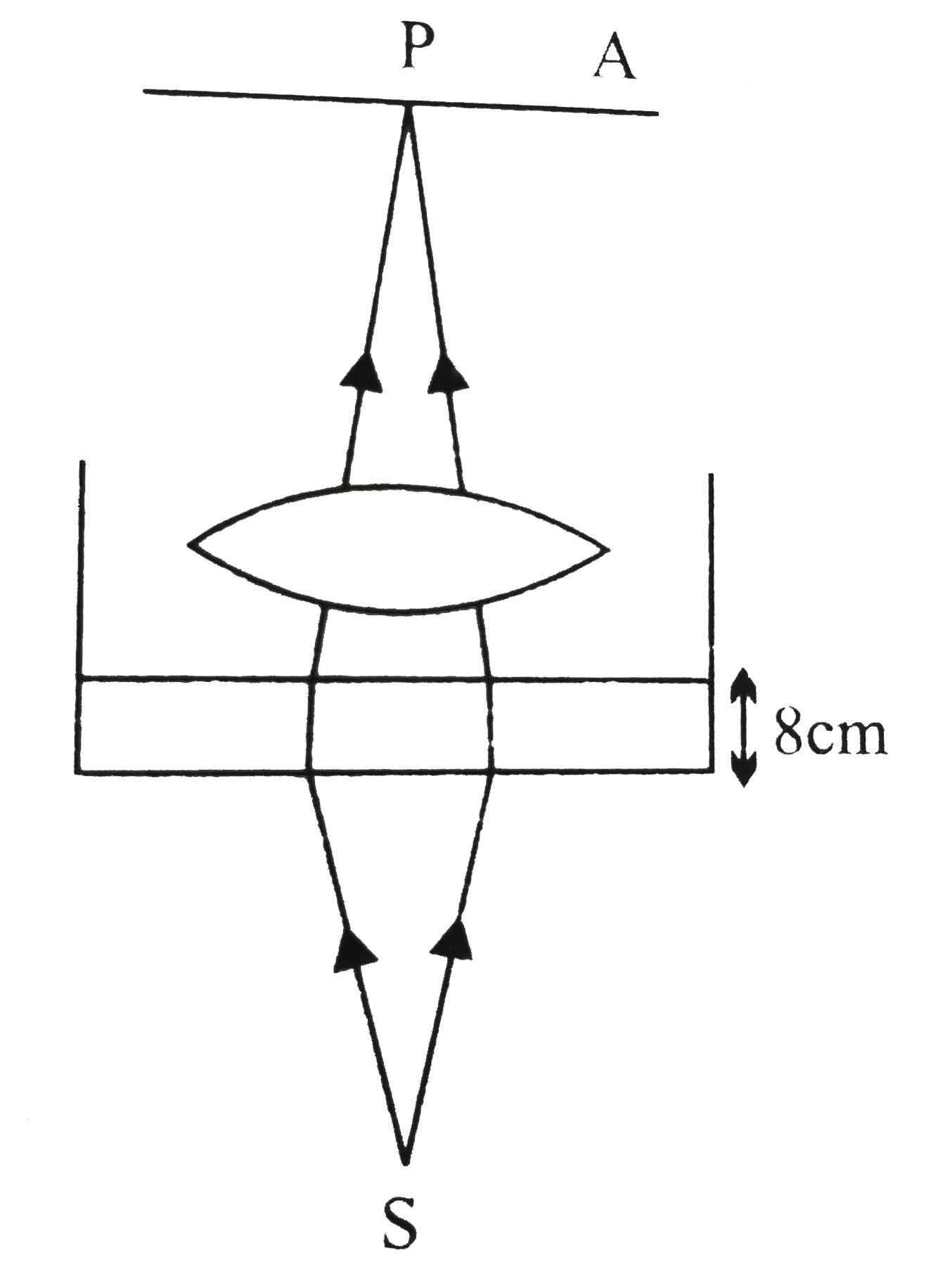
View SolutionThe distance between two point sources of light is 24cm. Find out where would you place a converging lens of focal length 9cm, so that the images of both the sources are formed at the same point.
View Solution
