Time taken by sunlight to pass through a window of thickness 4mm whose refraactive index is 32, is
2×10−4S
2×10−8S
2×10−11S
2×1011S
The correct Answer is:C
To find the time taken by sunlight to pass through a window of thickness 4 mm with a refractive index of 32, we can follow these steps:
Step 1: Convert thickness to meters
The thickness of the window is given as 4 mm. We need to convert this to meters for consistency in units.
Thickness=4mm=4×10−3m
Step 2: Determine the speed of light in glass
The speed of light in a medium can be calculated using the formula:
vg=cμ
Where:
- c is the speed of light in vacuum, approximately 3×108m/s
- μ is the refractive index of the medium, which is 32 in this case.
Substituting the values:
vg=3×10832=3×108×23=2×108m/s
Step 3: Calculate the time taken to pass through the window
The time taken t to pass through the window can be calculated using the formula:
t=Thicknessvg
Substituting the values we have:
t=4×10−32×108
Step 4: Simplify the expression
Now, we simplify the expression:
t=42×10−3×10−8=2×10−11s
Final Result
The time taken by sunlight to pass through the window is:
t=2×10−11s
---
The thickness of the window is given as 4 mm. We need to convert this to meters for consistency in units.
The speed of light in a medium can be calculated using the formula:
- c is the speed of light in vacuum, approximately 3×108m/s
- μ is the refractive index of the medium, which is 32 in this case.
The time taken t to pass through the window can be calculated using the formula:
Now, we simplify the expression:
The time taken by sunlight to pass through the window is:
Similar Questions
Time taken by the sunlight to pass thought a slab of 4 cm and reflective index 1.5 is……….. S.
View SolutionThe time taken by a monochromatic light to travel a certain distance in air in 9×10−6 seconds. The time taken by the light ray to travel the same distance in water of refractive index 43 is
View SolutionThe time required for the light to pass through a glass slab ( refractive index=1.5) of thickness 4 mm is (c=3×108ms−1 speed of light in free space)
View SolutionTwo parallel rays are travelling in a medium of refractive index μ1=4/3. One of the rays passes through a parallel glass slab of thickness t and refractive index μ2=3/2. The path difference between the two rays due to the glass slab will be
View SolutionAn object is seen through a glass slab of thickness 36cm and refractive index 3/2. The observer, and the slab are dipped in water (μ=4/3). The shift produced in the position of the object is
View SolutionIn a modified YDSE, the region between the screen and slits is immersed in a liquid whose refractive index varies with time as μ1=(5/2)−(T/4) until it reaches s steady state value of 5/4. A glass plate of thickness 36 μm and refractive index 3/2 is introduced in front of one of the slits.
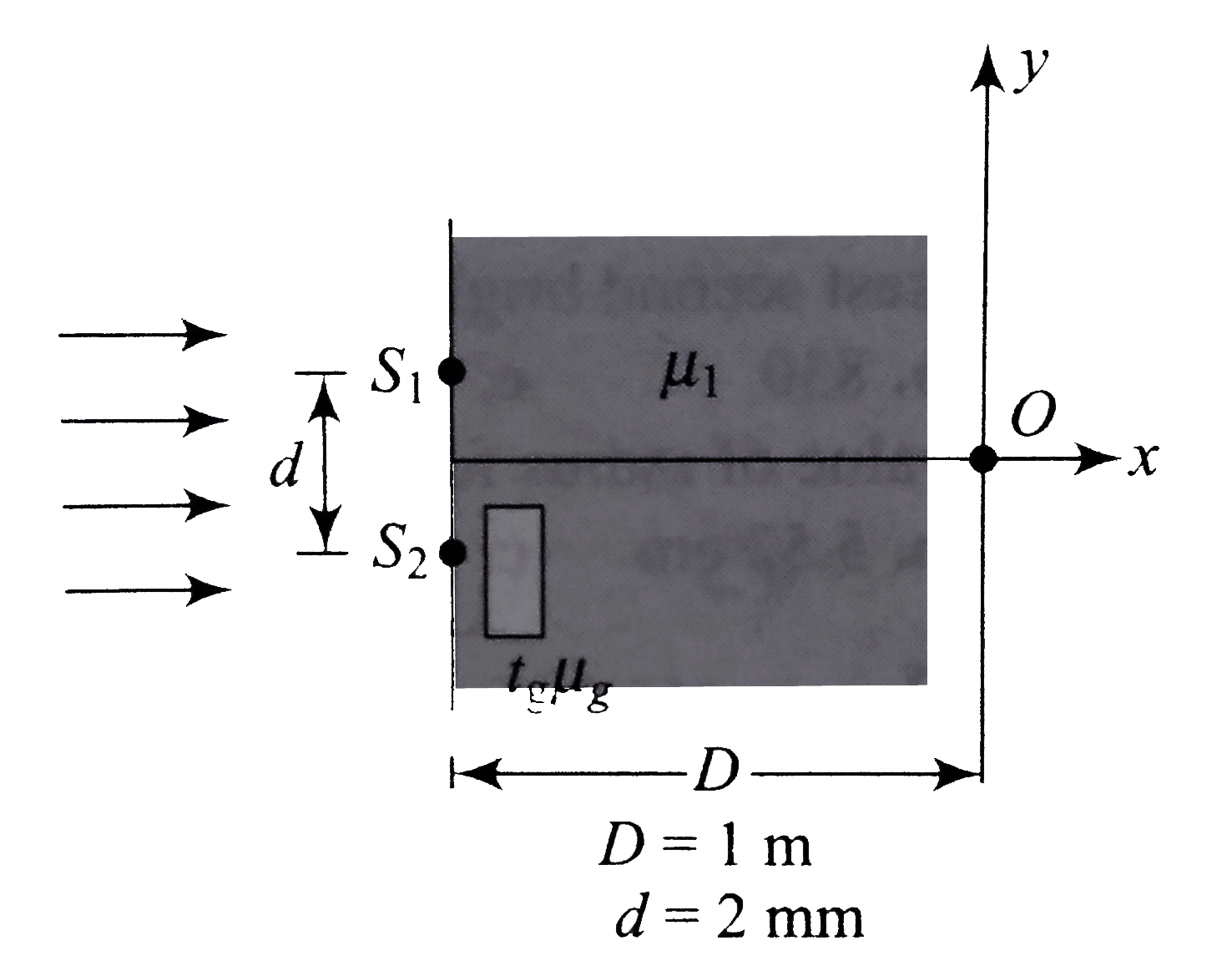
Find the time when central maxima is at point O. located symmetrically on the x-asix.
View SolutionLight travels through a glass plate of thickness t and refractive index μ. If c is the speed of light in vacuum, the time taken by light to travel this thickness of glass is
View SolutionThe ratio of thickness of plates of two transparent medium A and B is 6 : 4. If light takes equal time in passing through them, then refractive index of A with respect to B will be
View SolutionCalculate the time taken for a disturbance to pass through a string of length I and of mass per unit length m when the tension in the string is mI2gN.
View SolutionA ray of light is icncident at anangle of 60∘ on one face of a ractangular glass slab of thickness 2√3 mm refractive index √3 , Calculate the lateral shift produced in mm.
View Solution
