For photoelectric emission from certain metal the cut - off frequency is v. If radiation of frequency 2v incident on the metal plate , the maximum possible velocity of the emitted electron will be (m is the electron mass).
(a)(√hv2m)
(b)(√2hvm)
(c) √2hvm
(d) 2(√hvm)
The correct Answer is:C
To solve the problem of finding the maximum possible velocity of emitted electrons when radiation of frequency 2v is incident on a metal with a cut-off frequency v, we can follow these steps:
1. Identify the Work Function:
The work function ϕ of the metal is defined as the minimum energy required to remove an electron from the metal surface. It can be expressed in terms of the cut-off frequency v:
ϕ=hv
where h is Planck's constant.
2. Energy of Incident Radiation:
The energy E of the incident radiation with frequency 2v can be calculated using the formula:
E=h⋅(2v)=2hv
3. Apply Einstein's Photoelectric Equation:
According to Einstein's photoelectric equation, the kinetic energy K.E. of the emitted electrons can be expressed as:
K.E.=E−ϕ
Substituting the expressions for E and ϕ:
K.E.=2hv−hv=hv
4. Relate Kinetic Energy to Velocity:
The kinetic energy of an emitted electron is also given by:
K.E.=12mv2max
where m is the mass of the electron and vmax is the maximum velocity of the emitted electron. Setting the two expressions for kinetic energy equal gives us:
12mv2max=hv
5. Solve for Maximum Velocity:
Rearranging the equation to solve for vmax:
v2max=2hvm
Taking the square root of both sides:
vmax=√2hvm
Final Answer:
The maximum possible velocity of the emitted electron is:
vmax=√2hvm
The work function ϕ of the metal is defined as the minimum energy required to remove an electron from the metal surface. It can be expressed in terms of the cut-off frequency v:
ϕ=hv
where h is Planck's constant.
The energy E of the incident radiation with frequency 2v can be calculated using the formula:
E=h⋅(2v)=2hv
According to Einstein's photoelectric equation, the kinetic energy K.E. of the emitted electrons can be expressed as:
K.E.=E−ϕ
Substituting the expressions for E and ϕ:
K.E.=2hv−hv=hv
The kinetic energy of an emitted electron is also given by:
K.E.=12mv2max
where m is the mass of the electron and vmax is the maximum velocity of the emitted electron. Setting the two expressions for kinetic energy equal gives us:
12mv2max=hv
Rearranging the equation to solve for vmax:
v2max=2hvm
Taking the square root of both sides:
vmax=√2hvm
The maximum possible velocity of the emitted electron is:
vmax=√2hvm
Similar Questions
The photoelectric threshold frequency of a metal is v. When light of frequency 4v is incident on the metal . The maximum kinetic energy of the emitted photoelectrons is
View SolutionThe frequency of incident light falling on a photosensitive metal plate is doubled, the KE of the emitted photoelectrons is
View Solution
Knowledge Check
The photoeletric threshold 4v is incident on the metal is v. When light of freqency 4v is incident on the metal, the maximum kinetic energy of the emitted photoelectron is
A4hvB3hvC5hvD5hv2
The threshold frequency for a certain metal is v0. When a certain radiation of frequency 2v0 is incident on this metal surface the maximum velocity of the photoelectrons emitted is 2×106ms−1. If a radiation of frequency 3v0, is incident on the same metal surface the maximum velocity of the photoelectrons emitted (in m.s−1 ) is
View SolutionWork function of nickel is 5.01 eV. When ultraviolet radiation of wavelength 200A is incident of it, electrons are emitted. What will be the maximum velocity of emitted electrons?
View SolutionPhotoelectric emission is observed from a metallic surface for frequencies v1 and v2 of the incident light rays (v1>v2). If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio of 1:k , then the threshold frequency of the metallic surface is
View SolutionPhotoelectric emission is observed from a metallic surface for frequencies v1 and v2 of the incident light rays (v1>v2). If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio of 1:k , then the threshold frequency of the metallic surface is
View SolutionThe maximum velocity of the photoelectrons emitted from the surface is v when light of frequency n falls on a metal surface. If the incident frequency is increased to 3n, the maximum velocity of the ejected photoelectrons will be
View SolutionThe threshold frequency for a certain metal is 3.3×1014 Hz. If light of frequency 8.2×1014 Hz is incident on the metal, predict the cut-off voltage for the photoelectric emission.
View SolutionIn the photoelectric effect experiment, if f is the frequency of radiation incident on the metal surface and I is the intensity of the intensity radiations, then match the following columns:
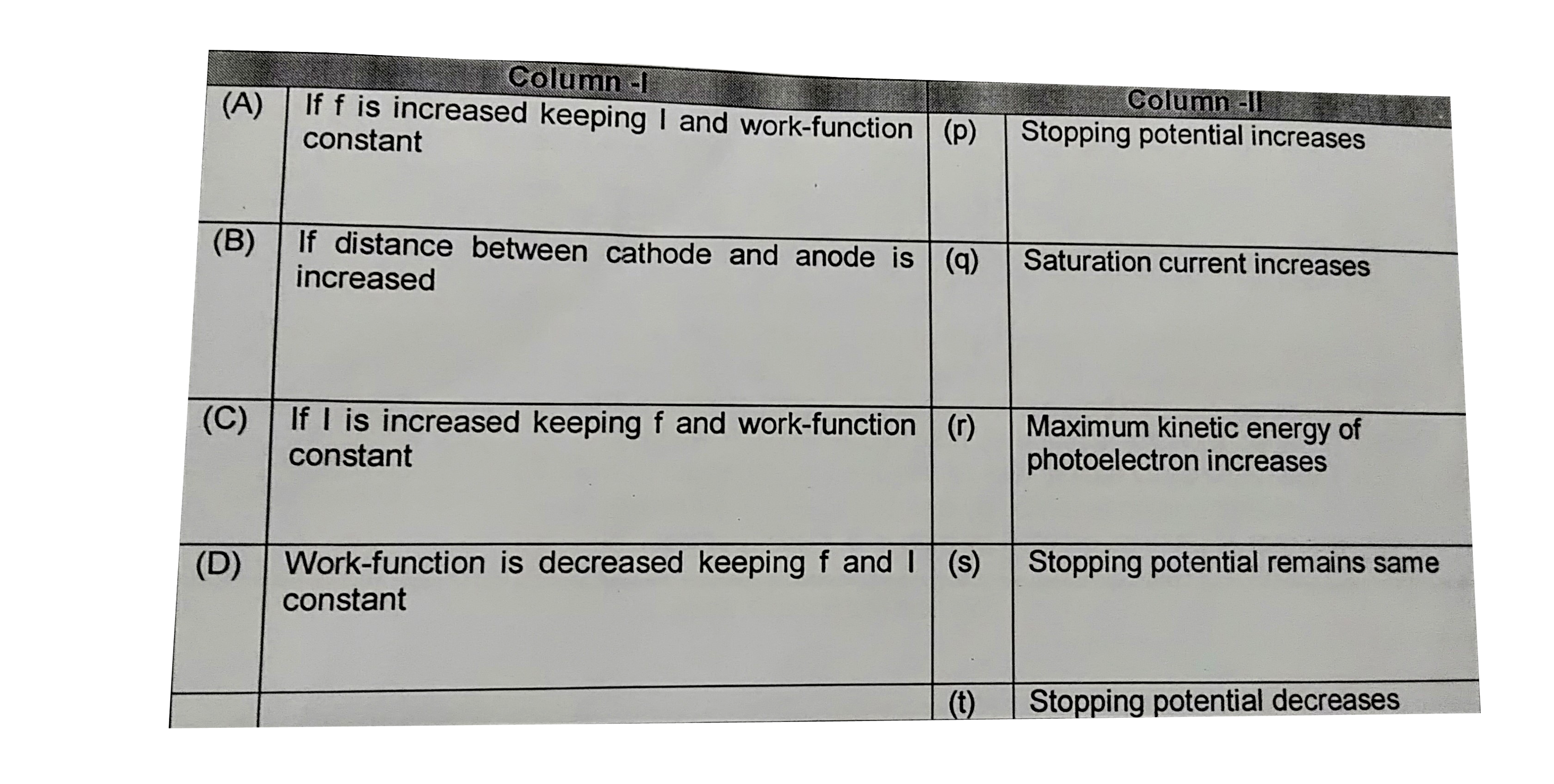
View Solution
