If α and β current gains in common-base and common-emitter configuration of a transistor, then β is equal to
1α
α1+α
α1−α
α−1α
The correct Answer is:C
To find the relationship between the current gains α (common-base current gain) and β (common-emitter current gain) in a transistor, we can follow these steps:
Step 1: Understand the definitions
- α is defined as the ratio of the collector current (IC) to the emitter current (IE) in a common-base configuration:
α=ICIE
- β is defined as the ratio of the collector current (IC) to the base current (IB) in a common-emitter configuration:
β=ICIB
Step 2: Relate the currents
In a transistor, the emitter current (IE) is the sum of the collector current (IC) and the base current (IB):
IE=IC+IB
Step 3: Substitute for IB
From the definition of β, we can express IB in terms of IC:
IB=ICβ
Step 4: Substitute IB into the equation for IE
Substituting IB into the equation for IE:
IE=IC+ICβ
Factoring out IC:
IE=IC(1+1β)
Step 5: Express IC in terms of IE
Now, we can express IC in terms of IE:
IC=IE1+1β=IEββ+1
Step 6: Substitute into the equation for α
Now, substituting IC into the equation for α:
α=ICIE=IEββ+1IE
This simplifies to:
α=ββ+1
Step 7: Solve for β
To find β in terms of α, we can rearrange the equation:
α(β+1)=β
Expanding and rearranging gives:
αβ+α=β
β−αβ=α
Factoring out β:
β(1−α)=α
Finally, solving for β:
β=α1−α
Final Answer
Thus, the relationship between β and α is:
β=α1−α
- α is defined as the ratio of the collector current (IC) to the emitter current (IE) in a common-base configuration:
α=ICIE
- β is defined as the ratio of the collector current (IC) to the base current (IB) in a common-emitter configuration:
β=ICIB
In a transistor, the emitter current (IE) is the sum of the collector current (IC) and the base current (IB):
IE=IC+IB
From the definition of β, we can express IB in terms of IC:
IB=ICβ
Substituting IB into the equation for IE:
IE=IC+ICβ
Factoring out IC:
IE=IC(1+1β)
Now, we can express IC in terms of IE:
IC=IE1+1β=IEββ+1
Now, substituting IC into the equation for α:
α=ICIE=IEββ+1IE
This simplifies to:
α=ββ+1
To find β in terms of α, we can rearrange the equation:
α(β+1)=β
Expanding and rearranging gives:
αβ+α=β
β−αβ=α
Factoring out β:
β(1−α)=α
Finally, solving for β:
β=α1−α
Thus, the relationship between β and α is:
β=α1−α
Similar Questions
In a common-base configuration of a transistor ΔiΔie=0.98, then current gain in common emitter configuration of transistor will be
View SolutionThe current gain for a transistor used in common - emitter configuration is 98. If the load resistance be 1MΩ and the internal resistance be 600Ω , what is the voltage gain ?
View Solution
Knowledge Check
If αandβ are the current gain in the CB and CE configurations respectively of the transistor circuit, then β−ααβ=
AzeroB1C2D5
In the following common emitter configuration an NPN transistor with current gain β=100 is used. The output voltage of the amlifier will be
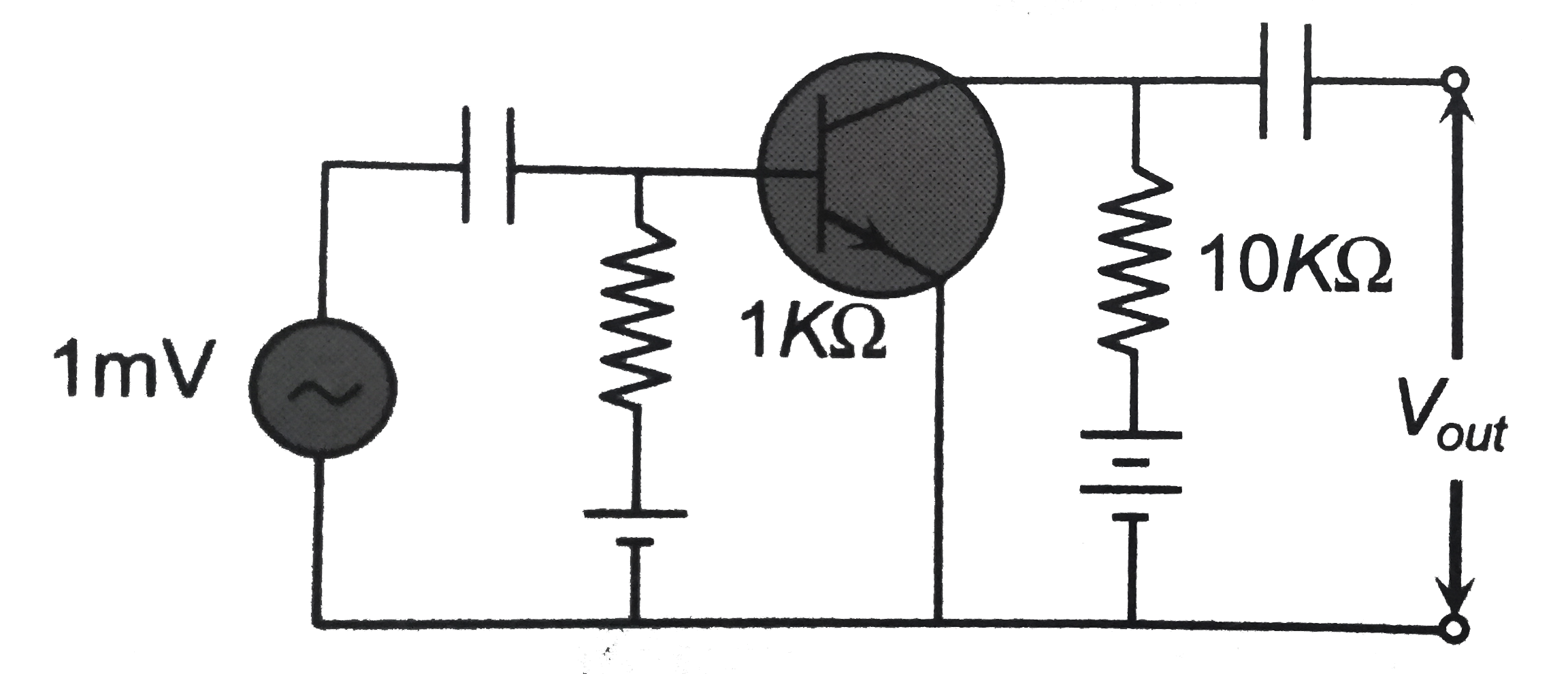
View SolutionIn the following common emitter configuration an NPN transistor with current gain β=100 is used. The output voltage of the amlifier will be

View SolutionThe a-c current gain of a transistor is β=19. In its common-emitter configuration, what will be the change in the collector-current for a change of 0.4 mA in the base-current? What will be the change in the emitter current?
View SolutionIn the following common emitter configuration an n-p-n transistor with current gain β=100 is used. What is the output voltage of the amplifier ?
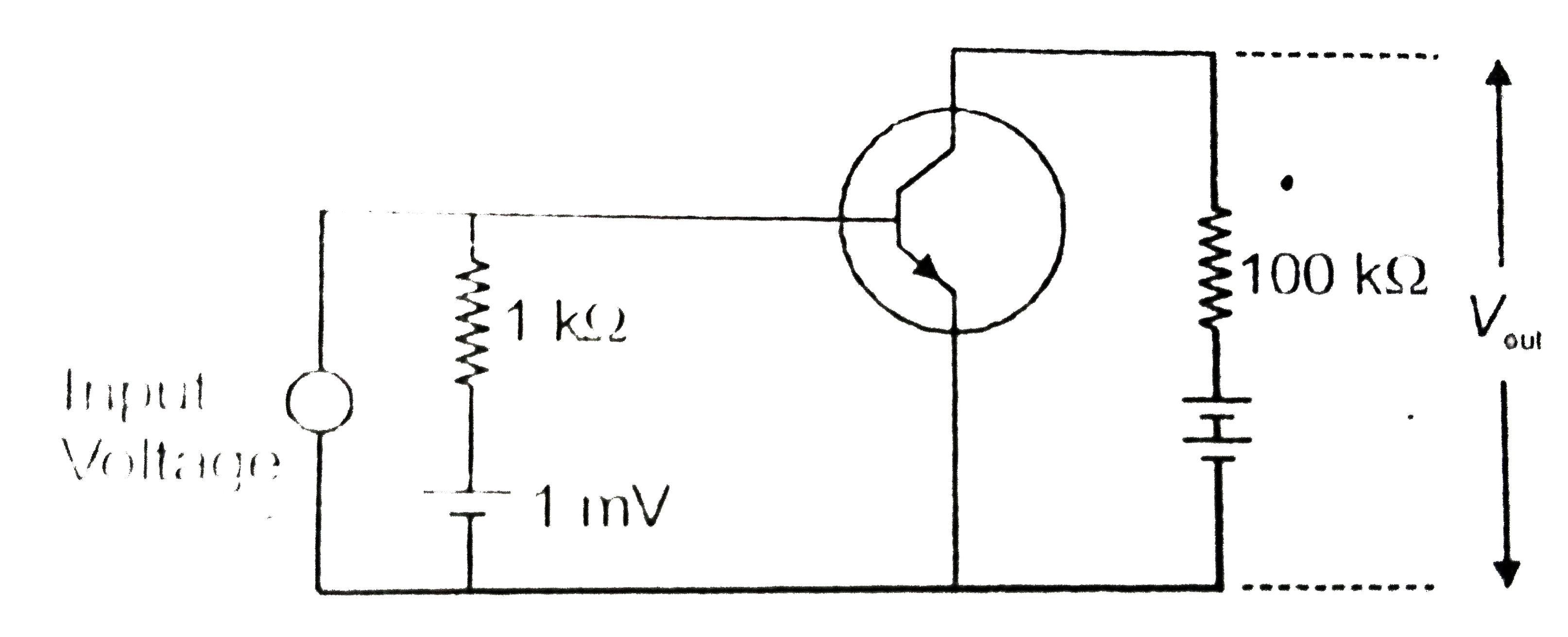
View SolutionIn common - emitter configuration of a transistor, the base current IE=2μA,α=0.9 then the value of IC is
View SolutionFor a transistor ICIE=0.96, then current gain for common emitter configuration
View SolutionFor a transistor ICIE=0.96, then current gain for common emitter configuration
View Solution
