For the reaction products, it is observed that:
(1) on doubling the initial concentration of only, the rate of reaction is also doubled and
(2) on doubling te initial concentration of both and , there is a charge by a factor of in the rate of the reaction.
The rate of this reaction is given by
The correct Answer is:B
To determine the rate law for the reaction A+B→products, we will analyze the information provided step by step.
Step 1: Understand the first observation
The first observation states that when the concentration of A is doubled, the rate of the reaction is also doubled. This implies that the rate of reaction is directly proportional to the concentration of A.
Mathematically, we can express this as:
Rate=k(A)m(B)n
where k is the rate constant, and m and n are the orders of the reaction with respect to A and B respectively.
From the first observation:
- If we double (A) (i.e., (A)→2(A)), the rate also doubles:
2⋅Rate=k(2(A))m(B)n
This simplifies to:
2⋅Rate=2mk(A)m(B)n
Since the original rate is k(A)m(B)n, we can equate:
2=2m
This implies m=1. Thus, the reaction is first order with respect to A.
Step 2: Understand the second observation
The second observation states that when the concentrations of both A and B are doubled, the rate of reaction increases by a factor of 8.
Using the rate law we established:
Rate=k(A)m(B)n
If we double both (A) and (B):
Rate′=k(2(A))m(2(B))n=k(21(A))(2n(B))=k⋅2m⋅2n⋅(A)m⋅(B)n
Substituting m=1:
Rate′=k⋅21⋅2n⋅(A)1⋅(B)n=21+n⋅k(A)(B)n
According to the second observation, this new rate is 8 times the original rate:
Rate′=8⋅Rate=8⋅k(A)(B)n
Equating the two expressions for Rate′:
21+n⋅k(A)(B)n=8⋅k(A)(B)n
Dividing both sides by k(A)(B)n (assuming (A) and (B) are not zero):
21+n=8
Since 8=23, we have:
1+n=3⟹n=2
Thus, the reaction is second order with respect to B.
Conclusion
Combining the orders we found:
- The reaction is first order with respect to A (i.e., m=1)
- The reaction is second order with respect to B (i.e., n=2)
Therefore, the rate law for the reaction A+B→products is:
Rate=k(A)1(B)2
Final Answer
Rate=k(A)(B)2
The first observation states that when the concentration of A is doubled, the rate of the reaction is also doubled. This implies that the rate of reaction is directly proportional to the concentration of A.
Rate=k(A)m(B)n
where k is the rate constant, and m and n are the orders of the reaction with respect to A and B respectively.
- If we double (A) (i.e., (A)→2(A)), the rate also doubles:
2⋅Rate=k(2(A))m(B)n
This simplifies to:
2⋅Rate=2mk(A)m(B)n
Since the original rate is k(A)m(B)n, we can equate:
2=2m
This implies m=1. Thus, the reaction is first order with respect to A.
The second observation states that when the concentrations of both A and B are doubled, the rate of reaction increases by a factor of 8.
Rate=k(A)m(B)n
If we double both (A) and (B):
Rate′=k(2(A))m(2(B))n=k(21(A))(2n(B))=k⋅2m⋅2n⋅(A)m⋅(B)n
Substituting m=1:
Rate′=k⋅21⋅2n⋅(A)1⋅(B)n=21+n⋅k(A)(B)n
According to the second observation, this new rate is 8 times the original rate:
Rate′=8⋅Rate=8⋅k(A)(B)n
Equating the two expressions for Rate′:
21+n⋅k(A)(B)n=8⋅k(A)(B)n
Dividing both sides by k(A)(B)n (assuming (A) and (B) are not zero):
21+n=8
Since 8=23, we have:
1+n=3⟹n=2
Thus, the reaction is second order with respect to B.
Combining the orders we found:
- The reaction is first order with respect to A (i.e., m=1)
- The reaction is second order with respect to B (i.e., n=2)
Rate=k(A)1(B)2
Rate=k(A)(B)2
Similar Questions
In a reaction A + B → Products
(i) If the initial concentration of A is doubled and B is kept constant, the rate of the reaction is doubled
(ii) If the initial concentration both A and B are doubled the rate of reaction becomes eight times
The rate law of the reaction is :
View SolutionFor a reaction 2A+B→ Products, doubling the initial concentration of both the reactants increases the rate by a factor of 8, and doubling the concentration of B alone doubles the rate. The rate law for the reaction is:
View Solution
Knowledge Check
If initial concentration is doubled, the time for half-reaction is also doubled, the order of reaction is
AzeroBfirstCsecondDthird
For the reaction A+B→C+D, doubling the concentration of both the reactants increases the reaction rate by 8 times and doubling the initial concentration of only B ismply doubles the reaction rate. What is the rate law for the reaction ?
View SolutionFor a 1st order reaction if concentration is doubled then rate of reaction becomes
View SolutionFor a reaction of type A+B→ products it is observed that doubling concentration of A causes the reaction rate to be four times as great, but doubling amount of B does not affect the rate,The rate equation is
View SolutionFor a first order reaction, the rate of the reaction doubled as the concentration of the reactant is doubled.
View SolutionFor a hypothetical reaction, A+B→C+D, the rate =k[A]−1/2[B]3/2. On doubling the concentration of A and B the rate will be
View SolutionIn a reaction between A and B, the initial rate of reaction was measured for different initial concentrations of A and B as given below:
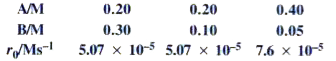
What is the order of reaction with respect to A and B ?
View SolutionIn a reaction between A and B, the initial rate of reaction was measured for different initial concentrations of A and B as given below:
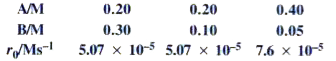
What is the order of reaction with respect to A and B ?
View Solution
