A child is swinging a swing. Minimum and maximum heights fo swing from the earth's surface are 0.75 m and 2 m respectively. The maximum velocity of this swing is
10 m/s
5 m/s
8 m/s
15 m/s
The correct Answer is:B
To find the maximum velocity of the swing, we can use the principle of conservation of mechanical energy. The potential energy at the maximum height will be converted into kinetic energy at the lowest point of the swing.
1. Identify the heights:
- Minimum height (h1) = 0.75 m
- Maximum height (h2) = 2 m
2. Calculate the change in height (Δh):
Δh=h2−h1=2m−0.75m=1.25m
3. Apply the conservation of energy:
The potential energy at the maximum height (h2) will be equal to the kinetic energy at the minimum height (h1).
mgh2=12mv2max
Here, m is the mass of the child (which will cancel out), g is the acceleration due to gravity (approximately 9.81m/s2), and vmax is the maximum velocity.
4. Rearranging the equation:
Since we are interested in vmax, we can rearrange the equation:
v2max=2g(h2−h1)
5. Substituting the values:
v2max=2g(1.25)
v2max=2×9.81×1.25
6. Calculating v2max:
v2max=24.525m2/s2
7. Finding vmax:
vmax=√24.525≈4.95m/s
8. Final result:
The maximum velocity of the swing is approximately 5m/s.
- Minimum height (h1) = 0.75 m
- Maximum height (h2) = 2 m
Δh=h2−h1=2m−0.75m=1.25m
The potential energy at the maximum height (h2) will be equal to the kinetic energy at the minimum height (h1).
mgh2=12mv2max
Here, m is the mass of the child (which will cancel out), g is the acceleration due to gravity (approximately 9.81m/s2), and vmax is the maximum velocity.
Since we are interested in vmax, we can rearrange the equation:
v2max=2g(h2−h1)
v2max=2g(1.25)
v2max=2×9.81×1.25
v2max=24.525m2/s2
vmax=√24.525≈4.95m/s
The maximum velocity of the swing is approximately 5m/s.
Similar Questions
The minimum and maximum distance of a satellite from the centre of the earth are 2R and 4R respectively, where R is the radius of earth and M is the mass of the earth. The radius of curvature at the point of maximum distance is
View SolutionThe minimum and maximum velocities of a projectile are 10ms−1 and 20ms−1 respectively. The horizontal range and maximum height are respectively (g=10 ms−2)
View SolutionThe minimum and maximum distances of a satellite from the center of the earth are 2R and 4R respectively, where R is the radius of earth and M is the mass of the earth . Find
(a) its minimum and maximum speeds,
(b) radius of curvature at the point of minimum distance.
View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :
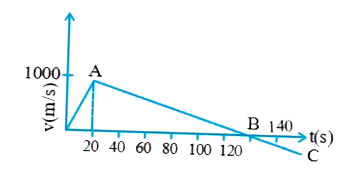
View SolutionMaximum height reached by a rocket fired with a speed equal to 50% of the escape velocity from earth's surface is:
View SolutionA particle is throws vertically upwards from the surface of earth and it reaches to a maximum height equal to the radius of earth. The radio of the velocity of projection to the escape velocity on the surface of earth is
View SolutionA mass m is taken to a height R from the surface of the earth and then is given a vertical velocity υ. Find the minimum value of υ, so that mass never returns to the surface of the earth. (Radius of earth is R and mass of the earth m).
View SolutionFind work done in shifting a body of mass m from a height h above the earth's surface to a height 2h above the earth's surface..
View SolutionThe minimum projection velocity of a body from the earth's surface so that it becomes the satellite of the earth (Re=6.4×106m).
View SolutionA simple pendulum with bob of mass m and conducting wire of length L swings under gravity through an angle 2θ. The earth's magnetic field component in the direction perpendicular to swing is B. The maximum potential difference induced across the pendulum is
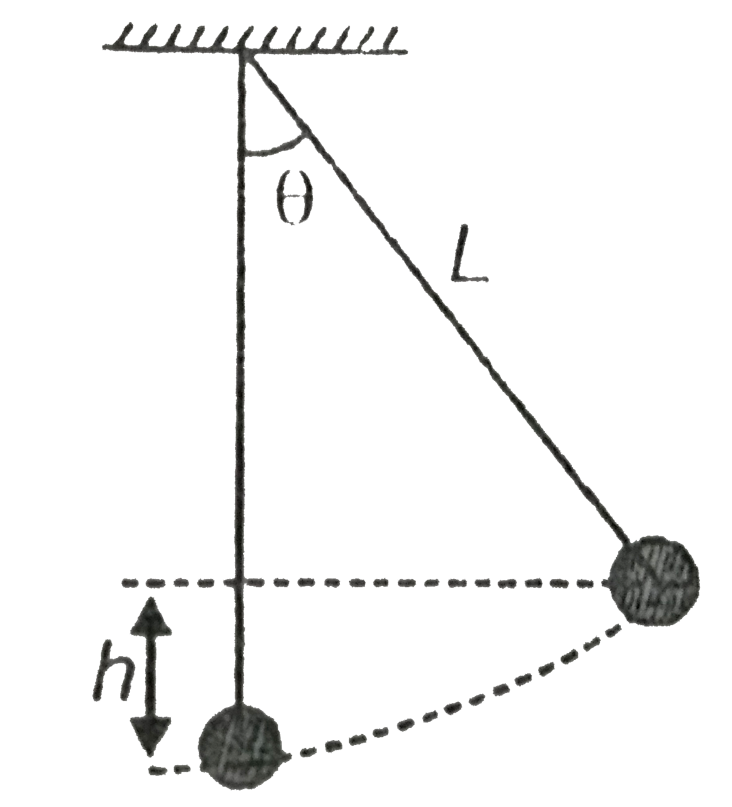
View Solution
