A point P consider at contact point of a wheel on ground which rolls on ground without sliping then value of displacement of point P when wheel completes half of rotation (If radius of wheel is 1m) : -
2m
√π2+4 m
π m
√π2+2 m
The correct Answer is:B
To solve the problem, we need to determine the displacement of point P, which is the contact point of a wheel with the ground, after the wheel has completed half of a rotation. Given that the radius of the wheel is r=1m, we can follow these steps:
1. Understand the Movement of the Wheel:
When the wheel rolls without slipping, the point of contact with the ground moves along with the wheel. After half a rotation, the point that was initially in contact with the ground will have moved to a new position.
2. Calculate the Distance Traveled by the Wheel:
The distance traveled by the wheel after half a rotation is equal to half of the circumference of the wheel. The circumference C of a circle is given by:
C=2πr
For a radius r=1m:
C=2π×1=2πm
Therefore, the distance traveled after half a rotation is:
Distance=12C=12×2π=πm
3. Determine the Final Position of Point P:
Initially, point P is at the bottom of the wheel (the contact point). After half a rotation, point P will have moved to the opposite side of the wheel, which is directly above the original contact point. The vertical distance from the ground to the top of the wheel is equal to the radius of the wheel, which is 1m.
4. Calculate the Displacement:
The displacement of point P is the straight-line distance from its initial position (at the bottom) to its final position (at the top). This can be visualized as a right triangle where:
- One leg is the distance traveled horizontally (which is πm),
- The other leg is the vertical distance (which is 1m).
Using the Pythagorean theorem to find the displacement d:
d=√(horizontal distance)2+(vertical distance)2
d=√(π)2+(1)2
d=√π2+1
5. Final Result:
The displacement of point P after the wheel completes half a rotation is:
d=√π2+1m
When the wheel rolls without slipping, the point of contact with the ground moves along with the wheel. After half a rotation, the point that was initially in contact with the ground will have moved to a new position.
The distance traveled by the wheel after half a rotation is equal to half of the circumference of the wheel. The circumference C of a circle is given by:
C=2πr
For a radius r=1m:
C=2π×1=2πm
Therefore, the distance traveled after half a rotation is:
Distance=12C=12×2π=πm
Initially, point P is at the bottom of the wheel (the contact point). After half a rotation, point P will have moved to the opposite side of the wheel, which is directly above the original contact point. The vertical distance from the ground to the top of the wheel is equal to the radius of the wheel, which is 1m.
The displacement of point P is the straight-line distance from its initial position (at the bottom) to its final position (at the top). This can be visualized as a right triangle where:
- One leg is the distance traveled horizontally (which is πm),
- The other leg is the vertical distance (which is 1m).
d=√(horizontal distance)2+(vertical distance)2
d=√(π)2+(1)2
d=√π2+1
The displacement of point P after the wheel completes half a rotation is:
d=√π2+1m
Similar Questions
If a given point P is in contact with ground initially and wheel of radius R is in pure rolling, then the displacement of point P when point P reaches topmost of the sphere for the first time will be
 View Solution
View SolutionA Wheel of circumference C is at rest on the ground.When the wheel rolls forward through half a revolution ,then the displacement of point contact will be
View Solution
Knowledge Check
- Question 1 - Select One
A wheel of mass 5kg and radius 0.40m is rolling on a road without sliding with angular velocity 10rads−1. The moment of ineria of the wheel about the axis of rotation is 0.65kgm2. The percentage of kinetic energy of rotate in the total kinetic energy of the wheel is.
A22.4%B11.2%C88.8%D44.8%
A wheel of radius R rolls on the ground with a uniform velocity v. The relative acceleration of topmost point of the wheel with respect to the bottommost point is:
View SolutionA wheel ios rolling without sliding on a horizontal surface. The centre of the wheelk moves with a constant speed v0. Consider a point P on the rim which is at the top at time t=0. The square of speed of point P is plooted against time t. The correct plot is (R is radius of the wheel)
View SolutionA wheel of radius 1m rolls forward half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially on contact with the ground is.
View SolutionA wheel of perimeter 4π is rolling on a horizontal surface. The displacement of the point of contact of wheel and ground when the wheel completes one quarter of revolution is
View SolutionA wheel of radius R rolls on the ground with a uniform velocity v. The velocity of topmost point relative to the bottommost point is
View SolutionConsider a wheel rolls without slipping and its centre moves with constant acceleration a. Find the acceleration of points O,P,Q and S when linear velocity of the centre of wheel is v.
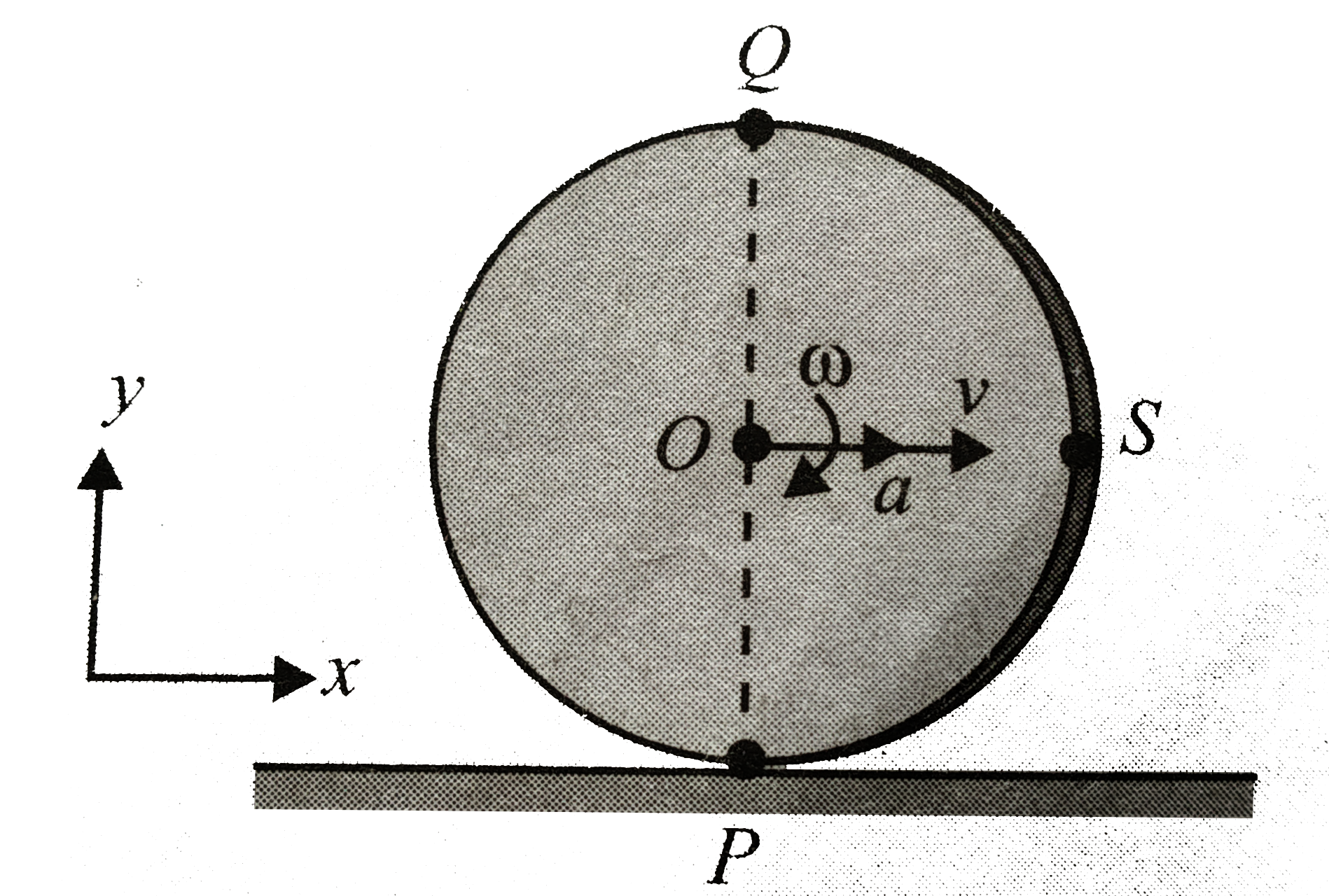 View Solution
View SolutionA wheel of radius 'R' is placed on ground and its contact point 'P'. If wheel starts rolling without slipped and completes half a revolution, find the displacement of point.
 View Solution
View Solution

