A train moving at a speed of 220ms−1 towards a stationary object emits a sound of frequency 1000 Hz. Some of the sound reaching the object gets reflected back to the train as echo. The frequency of the echo as detected by the driver of the train is (speed of sound in air is 330ms−1)
4000 Hz
5000 Hz
3000 Hz
3500 Hz
The correct Answer is:B
To solve the problem, we need to calculate the frequency of the echo as detected by the driver of the train. We will use the Doppler effect formula for sound waves.
1. Identify the Given Values:
- Speed of the train (VS) = 220 m/s (towards the stationary object)
- Frequency of the sound emitted by the train (F) = 1000 Hz
- Speed of sound in air (V) = 330 m/s
2. Determine the Frequency of Sound Reaching the Object:
When the train emits sound towards the stationary object, the frequency detected by the object can be calculated using the Doppler effect formula:
f′=F⋅V+VOV−VS
Here, VO (the speed of the observer) is 0 since the object is stationary. Thus, the formula simplifies to:
f′=F⋅VV−VS
3. Substituting the Values:
f′=1000⋅330330−220
f′=1000⋅330110
f′=1000⋅3=3000 Hz
4. Determine the Frequency of the Echo Detected by the Train:
Now, the sound reflected back from the object is perceived by the train. The train is now the observer moving towards the source of the sound (the object). We will use the Doppler effect formula again:
f′′=f′⋅V+VTV−VS
Here, VT is the speed of the train (220 m/s). So, we have:
f′′=3000⋅330+220330−220
f′′=3000⋅550110
f′′=3000⋅5=15000 Hz
5. Final Result:
The frequency of the echo as detected by the driver of the train is 15000 Hz.
- Speed of the train (VS) = 220 m/s (towards the stationary object)
- Frequency of the sound emitted by the train (F) = 1000 Hz
- Speed of sound in air (V) = 330 m/s
When the train emits sound towards the stationary object, the frequency detected by the object can be calculated using the Doppler effect formula:
f′=F⋅V+VOV−VS
Here, VO (the speed of the observer) is 0 since the object is stationary. Thus, the formula simplifies to:
f′=F⋅VV−VS
f′=1000⋅330330−220
f′=1000⋅330110
f′=1000⋅3=3000 Hz
Now, the sound reflected back from the object is perceived by the train. The train is now the observer moving towards the source of the sound (the object). We will use the Doppler effect formula again:
f′′=f′⋅V+VTV−VS
Here, VT is the speed of the train (220 m/s). So, we have:
f′′=3000⋅330+220330−220
f′′=3000⋅550110
f′′=3000⋅5=15000 Hz
The frequency of the echo as detected by the driver of the train is 15000 Hz.
Similar Questions
In the above problem, if some of the sound reaching the target ges reflected back to the rocket as an echo, then what frequency of the echo is detected by the rocket?
View SolutionA rocket is moving at a speed of 200ms−1 towards a stationary target. While moving, it emits a wave of frequency 1000 Hz. Some of the sound reaching the target gets reflected back to the racket as an echo. Calculate the frequency of sound as detected by the person at the position of target and frequency of echo as detected by the rocket . Given velocity of sound =330ms−1.
View Solution
Knowledge Check
- Question 1 - Select One
A train standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. The train begins to move with a speed of 30 ms−1 towards the platform. The frequency of the sound heard by an observer standing on the platform is
(Speed of sound in air = 330 m s−1)A420 HzB430 HzC440 HzD450 Hz
A rocket is moving at a speed of 220 ms−1 towards a stationary target. While moving, it emits a wave of frequency 500 Hz. What is the frequency of the sound as detected by the target?
View SolutionA car is moving with 90kmh−1 blows a horn of 150 Hz, towards a cliff. The frequency of the reflected sound heard by the driver will be (speed of sound in air is 340ms−1 )
View SolutionA railroad train is travelling at 30.0 m/s in still air. The frequency of the note emitted by the train whistle is 262 Hz. Speed of sound in air is 340 m/s.
View SolutionA bat emits ultrasonic sound of frequency 1000 kHz in air. If the sound meets a water surface, what is the wavelength of (i) the reflected sound, (ii) the transmitted sound ? Speed of sound in air is 340 ms−1 and in water 1486ms−1.
View SolutionA source of sound of frequency 1000 Hzmoves to the right with a speed of 50 m/s relative to the ground. To its right is a reflecting surface moving to the left as shown in figure. Speed of the sound in air is 330 m/s.
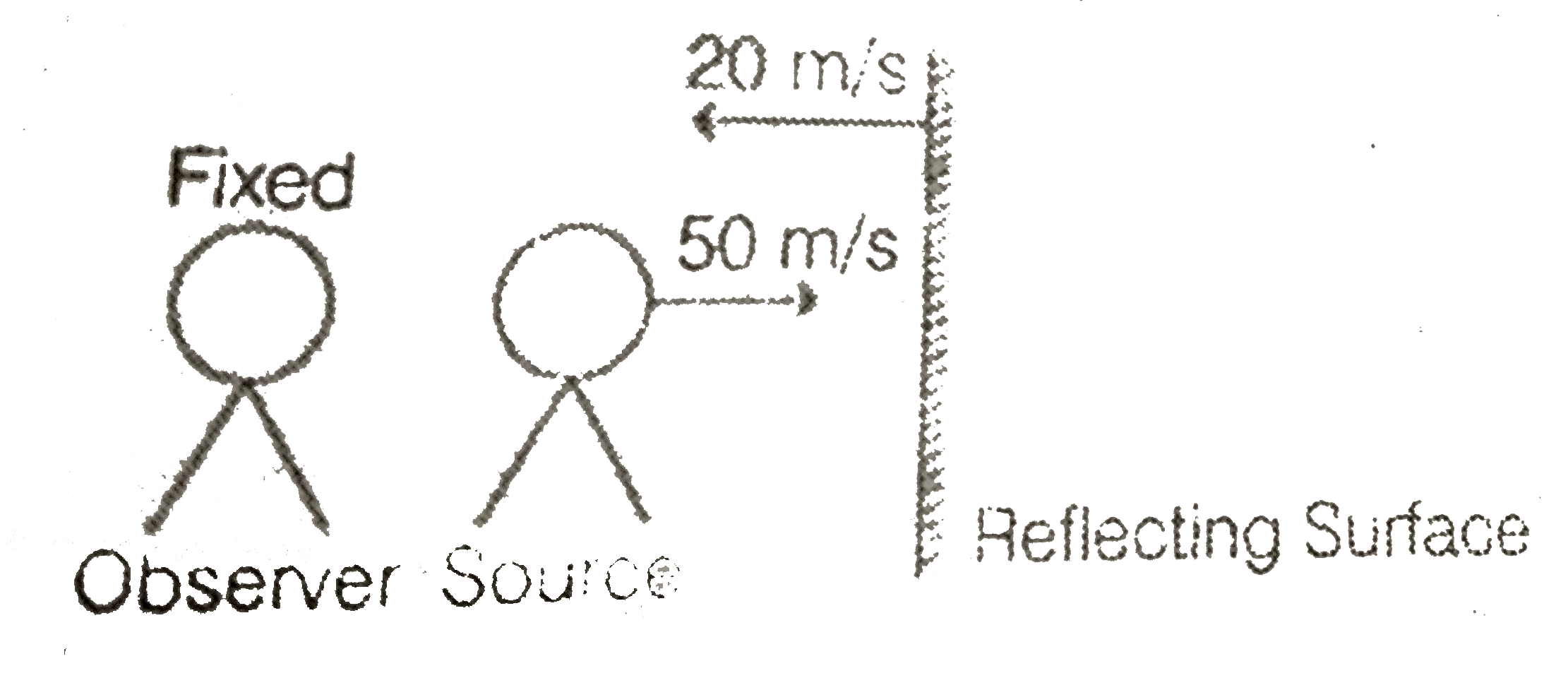
 View Solution
View SolutionA siren emitting a sound of frequency 800 Hz moves away from an observer towards a cliff at a speed of 15ms−1. Then the frequency of sound that the observer hears in the echo reflected from the cliff is (Take velocity of sound in air =330ms−1)
View SolutionA train is moving with a constant speed along a circular track. The engine of the train emits a sound of frequency f. The frequency heard by the guard at the rear end of the train.
View Solution

