If the bond dissociation energies of XY,X2 and Y2 are in the ratio of 1:1:0.5 and ΔHf for the formation of Xy is −200KJ/mol. The bond dissociation energy of X2 will be :−
800 KJ mol−1
100 KJ mol−1
200 KJ mol−1
400 KJ mol−1
The correct Answer is:A
To solve the problem, we need to find the bond dissociation energy of X2 given the bond dissociation energies of XY, X2, and Y2 in the ratio of 1:1:0.5 and the formation enthalpy ΔHf for XY as −200kJ/mol.
1. Define Bond Dissociation Energies:
Let the bond dissociation energy of XY be x. Then, according to the given ratio:
- Bond dissociation energy of X2=x
- Bond dissociation energy of Y2=0.5x
2. Write the Reaction for Formation of XY:
The formation of XY can be represented as:
12X2+12Y2→XY
3. Apply Hess's Law:
According to Hess's law, the enthalpy change for the reaction can be expressed as:
ΔH=(Bond energies of reactants)−(Bond energies of products)
For our reaction:
ΔHf=(12×x+12×0.5x)−x
4. Substitute the Known Value of ΔHf:
We know ΔHf=−200kJ/mol:
−200=(12x+14x)−x
5. Simplify the Equation:
Combine the terms:
−200=(34x)−x
This simplifies to:
−200=−14x
6. Solve for x:
Multiply both sides by -4:
800=x
7. Conclusion:
The bond dissociation energy of X2 is 800kJ/mol.
Final Answer:
The bond dissociation energy of X2 is 800kJ/mol.
Let the bond dissociation energy of XY be x. Then, according to the given ratio:
- Bond dissociation energy of X2=x
- Bond dissociation energy of Y2=0.5x
The formation of XY can be represented as:
12X2+12Y2→XY
According to Hess's law, the enthalpy change for the reaction can be expressed as:
ΔH=(Bond energies of reactants)−(Bond energies of products)
For our reaction:
ΔHf=(12×x+12×0.5x)−x
We know ΔHf=−200kJ/mol:
−200=(12x+14x)−x
Combine the terms:
−200=(34x)−x
This simplifies to:
−200=−14x
Multiply both sides by -4:
800=x
The bond dissociation energy of X2 is 800kJ/mol.
The bond dissociation energy of X2 is 800kJ/mol.
Similar Questions
Knowledge Check
The bond dissociation energies of X2,Y2andXY are in the ratio of 1:0.5:1.ΔH for the formation of XY is -200 kJ mol^(-1).Thebonddissociatione≠rgyofX_2 will be
A200kJmol−1B100kJmol−1C800kJmol−1D400kJmol−1Enthalpy change for the reaction,
4H(g)→2H2(g) is -869.6 kJ
The dissociation energy of H - H bond isA−869.6kJB+434.8kJC+217.4kJD−434.8kJ
AB,A2 and B2 are diatomic molecules. If the bond enthalpies of A2,AB and B2 are in the ratio 1:1:0.5 and the enthalpy of formation of AB from A2 and B2 is −100kJmol−1 , what is the bond enthalpy of A2 ?
View SolutionAB,A2 and B2 are diatomic molecules. If the bond enthalpies of A2,AB and B2 are in the ratio 1:1:0.5 and the enthalpy of formation of AB from A2 and B2 is −100kJmol−1 , what is the bond enthalpy of A2 ?
View SolutionIf bond energy of H2,F2 and HF are in the ratio 2:1:3 and ΔHa(H2)=400kJ/mol. Then ΔHf(HF) is :
View SolutionThe dissociation energies of H2andO2 are 104 and 118 kcal mol−1 respectively. The heat of reaction 12H2(g)+12O2(g)→O−H(g) is 10 kcal. The bond energy of O - H bond is
View Solution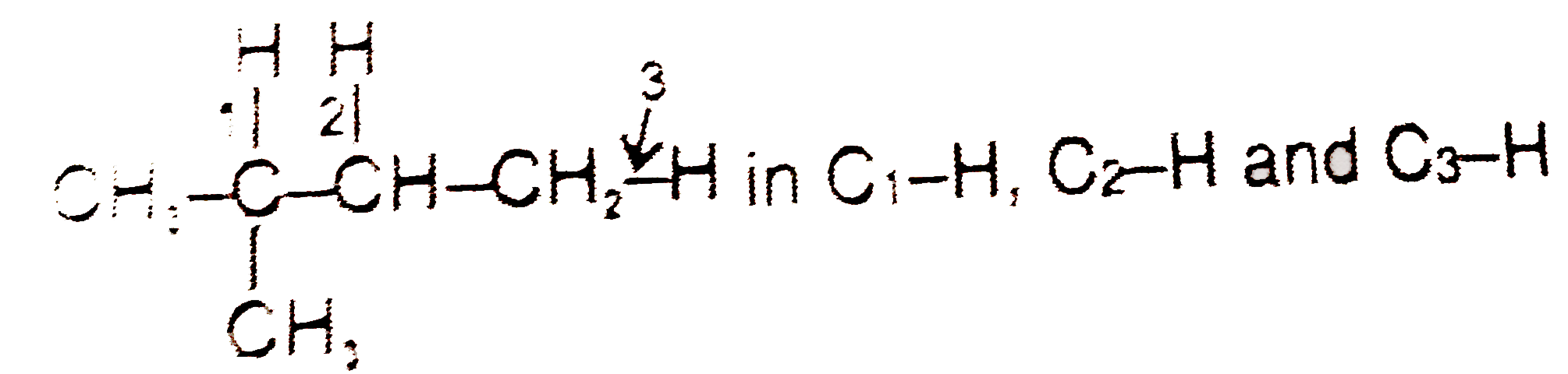 in C1−H,C2−H and C3−H the homolytic bond dissociation energy order is :
in C1−H,C2−H and C3−H the homolytic bond dissociation energy order is :
View SolutionFor Br2(l) Enthalpy of atomisation = x kJ/mol, Bond dissociation enthalpy of bromine = y kJ/mole, then
View Solution